>#Pytorch 卷积神经网络效果 [TOC] ## 数据与在线实践 tn2><a href="https://colab.research.google.com/drive/1qfRXFvWqBDfUpOzh2PUmjtvKC0i5OwFu?usp=sharing" target="_blank"><img alt="Google Colab" src="https://img.shields.io/badge/Open_the_colab-%23e87109?logo=https%3A%2F%2Fssl.gstatic.com%2Fcolaboratory-static%2Fcommon%2Facc37fa50857cc16c7a72c9c57f423f6%2Fimg%2Ffavicon.ico&link=https%3A%2F%2Fcolab.research.google.com%2Fdrive%2F1qfRXFvWqBDfUpOzh2PUmjtvKC0i5OwFu%3Fusp%3Dsharing"></a> 数据链接: https://pan.baidu.com/s/1VkrHDZGukkF900zLncMn5g 密码: 3lom ## 构建卷积神经网络 tn2>卷积网络中的输入和层与传统神经网络有些区别，需重新设计，训练模块基本一致 ```python import torch import torch.nn as nn import torch.optim as optim import torch.nn.functional as F # datasets 内置数据集 # transforms 做预处理操作 from torchvision import datasets,transforms import matplotlib.pyplot as plt import numpy as np %matplotlib inline ``` ## 首先读取数据 tn2>分别构建训练集和测试集（验证集） 使用DataLoader来迭代取数据。 ```python # 定义超参数 input_size = 28 #图像的总尺寸28*28 num_classes = 10 #标签的种类数 num_epochs = 3 #训练的总循环周期 batch_size = 64 #一个撮（批次）的大小，64张图片 # 训练集 train_dataset = datasets.MNIST(root='./data', train=True, transform=transforms.ToTensor(), download=True) # 测试集 test_dataset = datasets.MNIST(root='./data', train=False, transform=transforms.ToTensor()) # 构建batch数据 train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True) test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=True) ``` ## 卷积网络模块构建 tn2>一般卷积层，relu层，池化层可以写成一个套餐，接下来我将按照下面的神经网络图来进行构建我们的CNN模型。 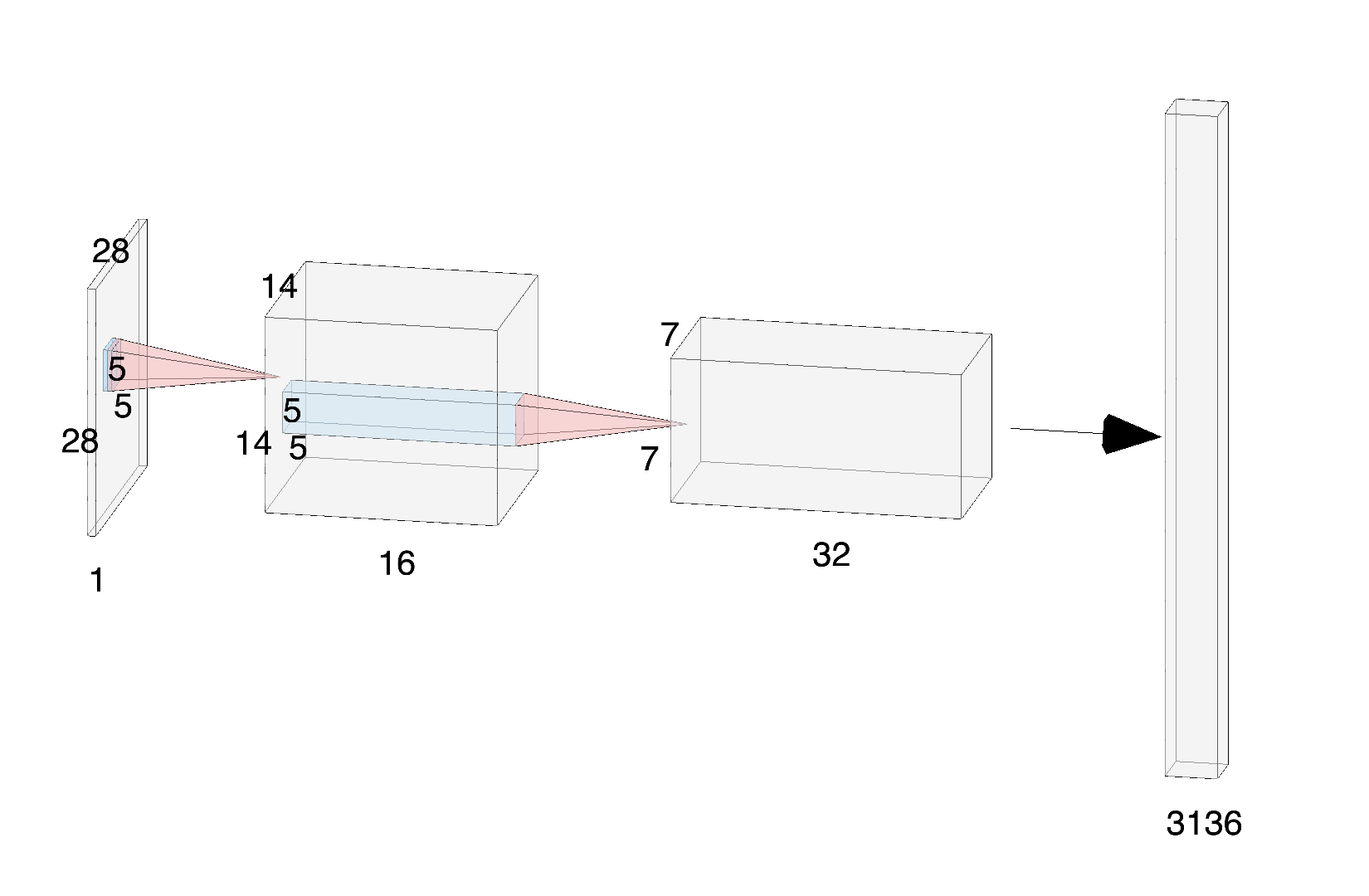 tn>注意卷积最后结果还是一个特征图，需要把图转换成向量才能做分类或者回归任务 ```python class CNN(nn.Module): def __init__(self): super(CNN, self).__init__() self.conv1 = nn.Sequential( # 输入大小 (1, 28, 28) Sequential 用于按顺序创建一个神经网络，依次堆叠不同的神经网络层 nn.Conv2d( # 2d卷积 in_channels=1, # 灰度图 out_channels=16, # 要得到几多少个特征图 kernel_size=5, # 卷积核大小 stride=1, # 步长 padding=2, # 如果希望卷积后大小跟原来一样，需要设置padding=(kernel_size-1)/2 if stride=1 ), # 输出的特征图为 (16, 28, 28) nn.ReLU(), # relu层 nn.MaxPool2d(kernel_size=2), # 进行池化操作（2x2 区域）, 输出结果为： (16, 14, 14) ) self.conv2 = nn.Sequential( # 下一个套餐的输入 (16, 14, 14) nn.Conv2d(16, 32, 5, 1, 2), # 输出 (32, 14, 14) nn.ReLU(), # relu层 nn.Conv2d(32, 32, 5, 1, 2), nn.ReLU(), nn.MaxPool2d(2), # 输出 (32, 7, 7) ) self.conv3 = nn.Sequential( # 下一个套餐的输入 (16, 14, 14) nn.Conv2d(32, 64, 5, 1, 2), # 输出 (32, 14, 14) nn.ReLU(), # 输出 (64, 7, 7) ) self.out = nn.Linear(64 * 7 * 7, 10) # 全连接层得到的结果 def forward(self, x): x = self.conv1(x) x = self.conv2(x) x = self.conv3(x) # 将原本的多维张量 x 重塑为一个二维张量，其第一个维度是批量大小，第二个维度是展平后的特征。 x = x.view(x.size(0), -1) # flatten操作，结果为：(batch_size, 32 * 7 * 7) output = self.out(x) return output ``` ## 评估标准 tn2>添加准确率作为评估标准 ```python def accuracy(predictions, labels): # torch.max 返回输入张量的最大值。这里我们使用它来获取预测概率最高的类别。 # predictions.data 是一个包含了模型输出的张量。 # torch.max 的第一个参数是要操作的张量，第二个参数 1 表示我们想要在每行中找到最大值（即每个样本的预测结果）。 # [1] 表示我们只关心最大值的索引（即预测的类别），而不是最大值本身。 pred = torch.max(predictions.data, 1)[1] # pred.eq(labels.data.view_as(pred)) 比较预测结果和真实标签。 # labels.data 是一个包含真实标签的张量。 # view_as(pred) 使 labels 的形状与 pred 相同。 # eq 函数比较两个张量，如果相同则返回1，不同则返回0。 # 因此这一行代码计算了正确预测的数量。 rights = pred.eq(labels.data.view_as(pred)).sum() # 返回正确预测的数量和总的标签数量。 # 这可以用于计算准确率：正确预测的数量 / 总标签数量。 return rights, len(labels) ``` ## 训练网络模型 ```python # 实例化 net = CNN() #损失函数 criterion = nn.CrossEntropyLoss() #优化器 optimizer = optim.Adam(net.parameters(), lr=0.001) #定义优化器，普通的随机梯度下降算法 #开始训练循环 for epoch in range(num_epochs): #当前epoch的结果保存下来 train_rights = [] for batch_idx, (data, target) in enumerate(train_loader): #针对容器中的每一个批进行循环 batch_idx是下标index net.train() # 训练模式 output = net(data) # 预测值 loss = criterion(output, target) # 计算损失值 optimizer.zero_grad() # 梯度清理 loss.backward() # 反向传播 optimizer.step() # 更新参数 right = accuracy(output, target) # 计算准确率 train_rights.append(right) # 保存 if batch_idx % 100 == 0: net.eval() # 测试模式 #测试集的准确率 val_rights = [] for (data, target) in test_loader: output = net(data) right = accuracy(output, target) val_rights.append(right) #准确率计算 train_r = (sum([tup[0] for tup in train_rights]), sum([tup[1] for tup in train_rights])) val_r = (sum([tup[0] for tup in val_rights]), sum([tup[1] for tup in val_rights])) print('当前epoch: {} [{}/{} ({:.0f}%)]\t损失: {:.6f}\t训练集准确率: {:.2f}%\t测试集正确率: {:.2f}%'.format( epoch, batch_idx * batch_size, len(train_loader.dataset), 100. * batch_idx / len(train_loader), loss.data, 100. * train_r[0].numpy() / train_r[1], 100. * val_r[0].numpy() / val_r[1])) ``` 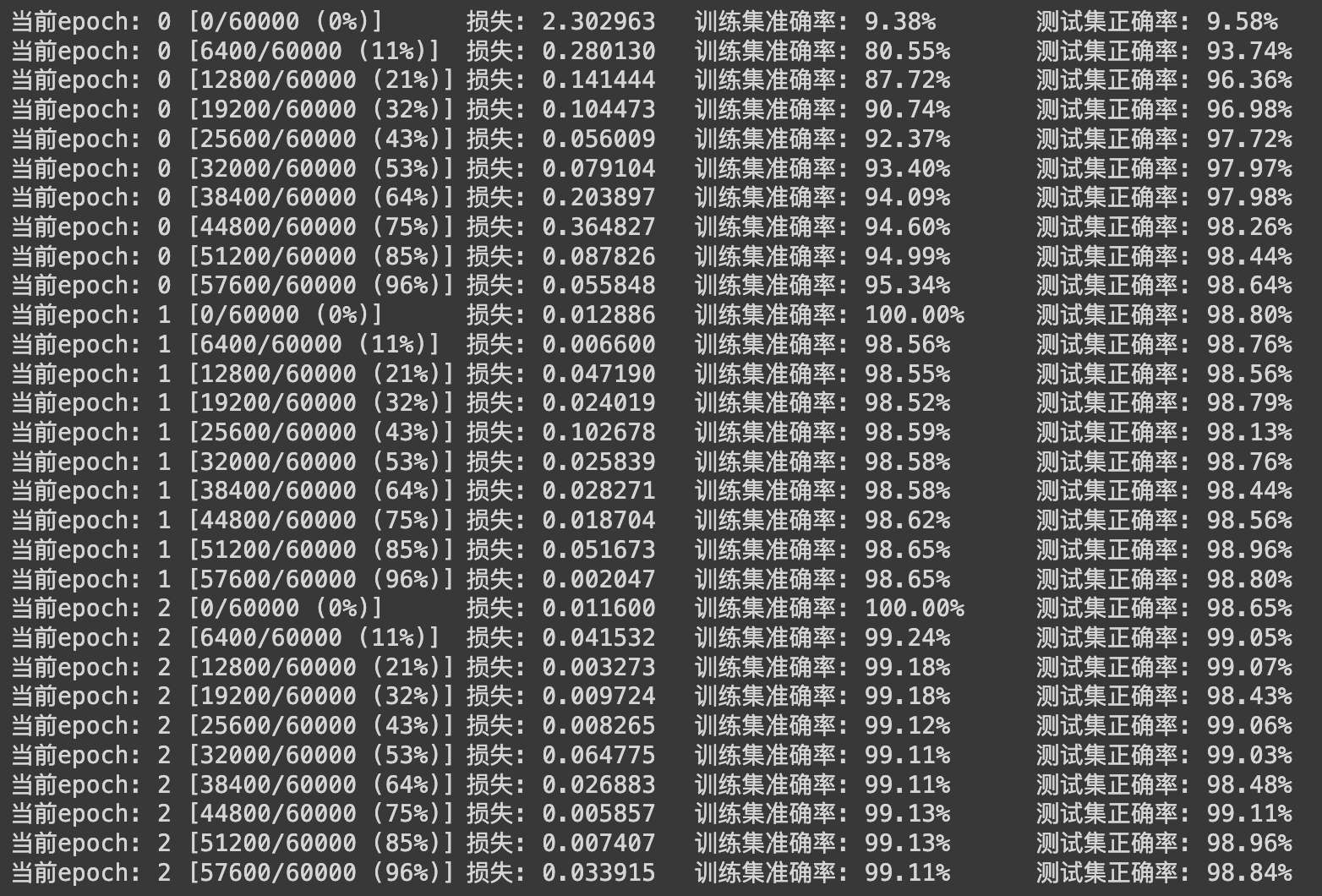 ## 总结 tn2>在此之后又加了一层卷积发现收敛的效果变慢了。 通过使用`3*3`的卷积核与`5*5`的卷积核对比，发现前者的刚开始训练的时候损失下降较高然后快速降低，后者刚开始损失下降比较明显然后缓慢下降。