>#Pytorch 自动求导与简单的线性回归 [TOC] ## 环境安装 tn2>安装pytorch ```python %pip install torch torchvision torchaudio ``` ## 自动计算反向传播 tn2>导入相关包 ```python import torch import numpy as np ``` tn2>需要求导的可以通过`requires_grad=True`开启自动求导。 ```python x = torch.randn(3, 4, requires_grad=True) x ``` >tensor([[-2.5528, 0.9500, 1.5432, 1.5304], [ 0.4176, -0.5373, -0.5960, 0.4130], [-0.7990, 0.5251, 0.0113, -0.4812]], requires_grad=True) ```python # 或者 x = torch.randn(3,4) x.requires_grad = True x ``` tn2>再举例一个简单的例子 ```python b = torch.randn(3, 4,requires_grad=True) # 第一个式子 t = x + b # 第二个式子 t的一个求和 y = t.sum() y ``` >tensor(-2.3695, grad_fn=<SumBackward0>) ```python # 进行反向传播 y.backward() ``` ```python # 查看b的梯度 b.grad ``` >tensor([[1., 1., 1., 1.], [1., 1., 1., 1.], [1., 1., 1., 1.]]) tn2>虽然没有指定t的`requires_grad`但是需要用到它，也会默认开启。 ```python x.requires_grad,b.requires_grad,t.requires_grad ``` >(True, True, True) ## 举个完整的例子 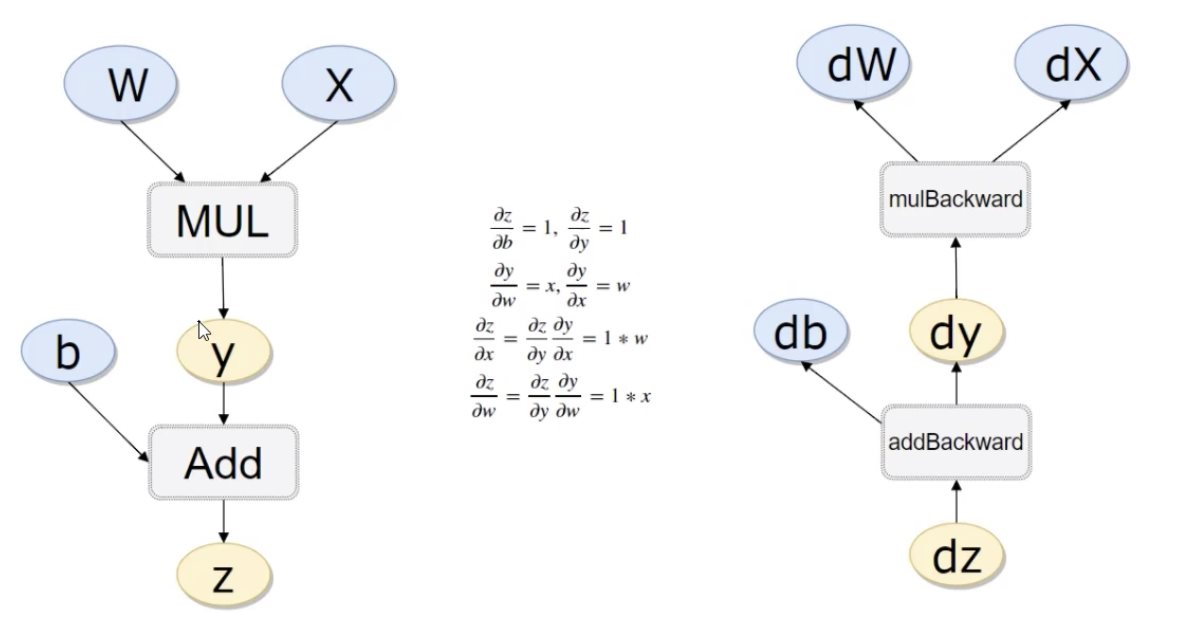 tn2>这幅图展示了一个简单的神经网络前向和反向传播的过程。 在前向传播部分（左侧）： 有两个输入节点，分别是 `W` 和 `X`，它们通过一个乘法操作（MUL）相乘得到 `y`。 `y` 之后和另一个节点 `b` 进行加法操作（Add），得到最终的输出 `z`。 在反向传播部分（右侧）： 反向传播用于计算损失函数（在这个例子中，假设 `z` 就是损失函数）相对于每个参数的梯度。 从 `z` 开始，假设对 `z` 进行求导，其导数 $$\frac{dz}{dz}$$ 自然是 1。 接下来计算 `z` 对 `b` 的导数 $$\frac{dz}{db}$$，因为 $$z = y + b$$，并且 `y` 是独立于 `b` 的，所以 $$\frac{dz}{db} = 1$$。 然后计算 `y` 对 `W` 的导数 $$\frac{dy}{dW}$$ 和 `y` 对 `X` 的导数 $$\frac{dy}{dX}$$，由于 $$y = W \times X$$，所以 $$\frac{dy}{dW} = X$$，$$\frac{dy}{dX} = W$$。 使用链式法则，计算 `z` 对 `W` 的导数 $$\frac{dz}{dW} = \frac{dz}{dy} \cdot \frac{dy}{dW} = 1 \times W = W$$，同理 $$\frac{dz}{dX} = \frac{dz}{dy} \cdot \frac{dy}{dX} = 1 \times X = X$$。 tn>在这个过程中，我们看到乘法操作（mulBackward）和加法操作（addBackward）的反向传播规则。每个节点上的导数值告诉我们，如果我们调整这个节点的值，输出 `z` 会如何改变。这些导数值在机器学习中被用来通过梯度下降算法更新参数 `W` 和 `b`，以最小化损失函数 `z`。 ```python # 计算流程 x = torch.rand(1) w = torch.rand(1, requires_grad=True) b = torch.rand(1, requires_grad=True) # 前向传播 y = x * w z = y + b ``` ```python x.requires_grad,w.requires_grad,b.requires_grad,y.requires_grad,z.requires_grad # 注意y也会进行自动求导 ``` >(False, True, True, True, True) ```python # 判断是否是叶子,叶子节点 x.is_leaf,w.is_leaf,b.is_leaf,y.is_leaf,z.is_leaf ``` >(True, True, True, False, False) tn2>反向传播计算 ```python z.backward(retain_graph=True) # retain_graph=True表示在反向传播后不要清理图,进行累计梯度 w.grad ``` >tensor([0.2982]) ```python b.grad ``` >tensor([2.]) ## 线性回归 tn2>线性回归是一种预测分析技术，用于研究两个连续变量之间的关系。它尝试通过最佳拟合直线来建模这种关系，这条直线是通过最小化实际数据点和预测数据点之间距离的平方和来确定的。这个过程被称为最小二乘法。线性回归可以是简单的（只有一个自变量）或多元的（多个自变量）。 构造一组输入数据x和其对应的标签y ```python # 创建一个包含0到10的整数列表 x_values = [i for i in range(11)] # 将列表转换为numpy数组，并指定元素类型为32位浮点数 x_train = np.array(x_values, dtype=np.float32) # 重新塑形数组为二维，其中每个原始元素都变成一行，形状变为(11, 1) x_train = x_train.reshape(-1, 1) # 打印出当前数组的形状，预期输出为(11, 1)，表示11行1列 x_train.shape,x_train ``` >((11, 1), array([[ 0.], [ 1.], [ 2.], [ 3.], [ 4.], [ 5.], [ 6.], [ 7.], [ 8.], [ 9.], [10.]], dtype=float32)) ```python y_values = [2*i + 1 for i in x_values] y_train = np.array(y_values, dtype=np.float32) y_train = y_train.reshape(-1, 1) y_train.shape,y_train ``` tn2>导入相关包 ```python import torch import torch.nn as nn import numpy as np ``` ## 线性回归模型 tn2>其实线性回归就是一个不加激活函数的全连接层。 ```python class LinearRegressionModel(nn.Module): def __init__(self, input_dim, output_dim): super(LinearRegressionModel, self).__init__() # 定义一个全连接层，指定使用到了哪些层 self.linear = nn.Linear(input_dim, output_dim) # 前向传播 def forward(self, x): out = self.linear(x) return out ``` ```python # 一个输入层 input_dim = 1 # 一个输出层 output_dim = 1 model = LinearRegressionModel(input_dim, output_dim) ``` ```python model ``` >LinearRegressionModel( (linear): Linear(in_features=1, out_features=1, bias=True) ) tn2>指定好参数和损失函数 ```python # 设置训练次数 epochs = 1000 # 设置学习率 learning_rate = 0.01 # 设置优化器 optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate) # 设置损失函数 criterion = nn.MSELoss() ``` tn2>训练模型 ```python for epoch in range(epochs): epoch += 1 # 注意转行成tensor inputs = torch.from_numpy(x_train) labels = torch.from_numpy(y_train) # 梯度要清零每一次迭代 optimizer.zero_grad() # 前向传播 outputs = model(inputs) # 计算损失 loss = criterion(outputs, labels) # 反向传播 loss.backward() # 更新参数权重 optimizer.step() if epoch % 50 == 0: print('epoch {}, loss {}'.format(epoch, loss.item())) ``` >epoch 50, loss 0.003172945464029908 epoch 100, loss 0.0018097275169566274 epoch 150, loss 0.0010321944719180465 epoch 200, loss 0.0005887215374968946 epoch 250, loss 0.00033578279544599354 epoch 300, loss 0.00019151577726006508 epoch 350, loss 0.00010923000081675127 epoch 400, loss 6.230236613191664e-05 epoch 450, loss 3.553432543412782e-05 epoch 500, loss 2.0268678781576455e-05 epoch 550, loss 1.1559625818335917e-05 epoch 600, loss 6.59192346574855e-06 epoch 650, loss 3.760904519367614e-06 epoch 700, loss 2.14508622775611e-06 epoch 750, loss 1.223156232299516e-06 epoch 800, loss 6.977222710702335e-07 epoch 850, loss 3.9789389916222717e-07 epoch 900, loss 2.2687767398110736e-07 epoch 950, loss 1.2930000536925945e-07 epoch 1000, loss 7.381613187362746e-08 tn2>测试模型预测结果 ```python predicted = model(torch.from_numpy(x_train)).detach().numpy() predicted ``` >array([[ 1.0005051], [ 3.0004325], [ 5.0003595], [ 7.0002866], [ 9.000215 ], [11.000142 ], [13.000069 ], [14.999996 ], [16.999924 ], [18.999851 ], [20.999779 ]], dtype=float32) tn2>模型的保存与读取 ```python # 保存 torch.save(model.state_dict(), 'model.pkl') ``` ```python # 读取 model.load_state_dict(torch.load('model.pkl')) ``` >`<All keys matched successfully>` tn2>使用gpu进行训练 ```python import torch import torch.nn as nn import numpy as np class LinearRegressionModel(nn.Module): def __init__(self, input_dim, output_dim): super(LinearRegressionModel, self).__init__() self.linear = nn.Linear(input_dim, output_dim) def forward(self, x): out = self.linear(x) return out input_dim = 1 output_dim = 1 model = LinearRegressionModel(input_dim, output_dim) # 判断是否有gpu如果有就带入 device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") model.to(device) epochs = 1000 learning_rate = 0.01 optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate) criterion = nn.MSELoss() for epoch in range(epochs): epoch += 1 # 使用gpu设备进行带入 inputs = torch.from_numpy(x_train).to(device) labels = torch.from_numpy(y_train).to(device) optimizer.zero_grad() outputs = model(inputs) loss = criterion(outputs, labels) loss.backward() optimizer.step() if epoch % 50 == 0: print('epoch {}, loss {}'.format(epoch, loss.item())) ```