>#人工智能数学基础补习题(微积分、定积分、牛顿--莱布尼茨公式) [TOC] ## 微积分简介 tn2>微积分是研究变化和积累的数学工具，它帮助我们理解事物如何变化以及如何累积量。 变化（微分）： 想象一辆汽车在移动，我们可能想知道它的速度是如何变化的。微积分可以帮助我们了解速度的变化，甚至可以推导出汽车的加速度（速度变化的变化）。 累积（积分）： 如果我们知道了汽车的速度变化，微积分可以帮助我们计算汽车移动的总距离。它可以处理累积问题，例如找出曲线下面积，这在许多实际问题中是很有用的，比如计算物体的总路径长度或总体积。 ## 定积分简介 tn2>定积分是微积分的一个重要概念，它主要用来解决曲线下面积的问题。 ## 牛顿--莱布尼茨公式 tn2>牛顿和莱布尼茨，独立发现的，因此以他们的名字命名。这个公式表达了定积分和微分之间的关系。 设函数 $$\(F(x)\)$$ 是连续的，并且在区间 $$\([a, b]\)$$ 上有一个原函数，即 \(F'(x) = f(x)\) ，其中 \(f(x)\) 是 \(F(x)\) 的导数。那么，曲线 \(y = f(x)\) 在区间 \([a, b]\) 上的定积分等于 $$\(F(b) - F(a)\)$$，即： $$\int_{a}^{b} f(x) \,dx = F(b) - F(a)$$ tn2>这意味着，如果你能找到一个函数 \(F(x)\)，其导数等于要积分的函数 \(f(x)\)，那么你就可以通过计算 \(F(b) - F(a)\) 来求解定积分。这个公式为我们提供了一种计算定积分的便捷方法。 这个公式在微积分中具有广泛的应用，使得我们可以更容易地从微分的角度来理解和处理定积分。 ## Python定积分求解方法 tn2>应用SciPy科学计算 $$\int_{0}^{3} cos^2 (e^x)dx$$ 0到3的曲线面积 ```python import numpy as np from scipy.integrate import quad func=lambda x:np.cos(np.exp(x)) **2 # 定义被积分函数 solution=quad(func,0,3) # 调用 quad 积分函数 print(solution) ``` >(1.296467785724373, 1.3977971863744082e-09) tn>二重积分：简单来讲求两个函数重叠部分的面积。 tn2>应用SciPy科学计算库 $$\iint_{D}e ^{-x^2-y^2} dxdy$$，其中$$ D={(x,y)|0\le x \le 10,0 \le y \le 10 } $$。 tn>在SciPy中的一般使用`dblquad`函数来进行二重积分.完整函数为`scipy.integrate.dblquad(func,a,b,gfun,hfun)`。 | 标签名 | 描述 | | ------------ | ------------ | | `func` | 是要积分的函数名称 | | `a` | 变量x的下限 | | `b` | 变量x的上线 | | `gfun` | 变量y的下线 | | `hfun` | 变量y的上线 | tn2>再本题中$$0\le y \le 10$$，即使y的下限和上限为常数，也要定义函数为`gfun(x)=0`、`hfun(x)=10`。 本题函数`gfun(x)`、`hfun(x)`的表达式为`lambda x:y_a`和`lambda x:y_b`，其中y_a、y_b的值为0和10。 ```python import numpy as np from scipy.integrate import dblquad def integrand(x,y): return np.exp(-x**2-y**2) x_a = 0 x_b = 10 y_a = 0 y_b = 10 solution,abserr = dblquad(integrand, x_a, x_b, lambda x :y_a, lambda x :y_b) print(solution,abserr) ``` >0.7853981633974476 1.3753098510194181e-08 tn2>应用python编程实现定积分求近似解，按照 $$\int_{0}^{3} cos^2 (e^x)dx$$ 进行求。 ```python from numpy import * a,b = 0,3 def f(x): return np.cos(np.exp(x)) **2 def trape(n): # 数值计算。输入参数 n 表示将积分区域分成 n 个小梯形 h=(b-a)/n # 计算每个小梯形的宽度，b 和 a 是积分区间的上下限 x=a # 初始化 x，表示当前小梯形的左边界 sum=0 # 初始化总和，用来累加每个小梯形的面积 # 使用循环计算每个小梯形的面积并累加 for i in range(1,n): x2=a+i*h # 计算当前小梯形的右边界 sum=sum+(f(x)+f(x2))*h/2 # 计算当前小梯形的面积并累加到总和 x=x2 # 更新 x，准备计算下一个小梯形 return sum ``` ```python a = 0 # 积分下限 b = 3 # 积分上限 n = 1000 # 分割数 # 定义被积函数 f = lambda x: np.cos(np.exp(x)) ** 2 # 使用梯形法则进行积分 approximate_result = trape(n) # 打印结果 print("梯形法则近似解：", approximate_result) ``` >梯形法则近似解： 1.2960750567338157 tn2>求积区间进行n=10，n=100，n=1000，n=100000等分，用来检验自定义的求定积分函数trape(n)的结果值。 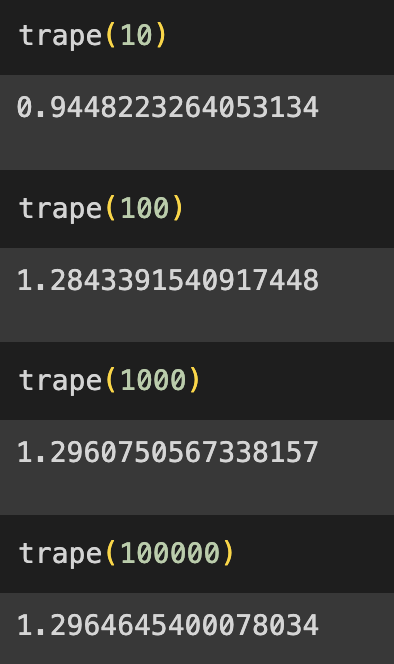 | 函数名 | 描述 | | ------------ | ------------ | | quad | 单积分 | | dblquad | 二重积分 | | tplquad | 三重积分 | | nquad | n倍多重积分 | | fixed_quad | 高斯积分，阶数为n | | quadrature | 高斯正交到容差 | | romberg | Romberg积分 | | trapz | 梯形规则 | | cumtrapz | 梯形法则累计计算积分 | | simps | 辛普森的规则 | | romb | Romberg积分 | | polyint | 分析多项式积分（NumPy） | | polyld | 辅助函数polyint（NumPy） | tn2>求使用牛顿--莱布尼茨下列定积分和极限值。 $$\int_{1}^{2} (x^2+\frac{1}{x^4})$$ ```python import sympy as sp # 定义变量和函数 x = sp.symbols('x') f = x**2 + 1/x**4 # 计算原函数 F = sp.integrate(f, x) # 计算在积分区间端点的原函数值 integral_value = F.subs(x, 2) - F.subs(x, 1) # 打印结果 print("定积分的值：", integral_value.evalf()) print("当趋近于无穷：", sp.limit(f,x,sp.oo)) print("当趋近于负无穷时：", sp.limit(f,x,-sp.oo)) print("当趋近于2时：", sp.limit(f,x,2)) ``` >定积分的值： 2.62500000000000 当趋近于无穷： oo 当趋近于负无穷时： oo 当趋近于2时： 65/16 tn2>使用numpy解决的方式。 ```python import numpy as np from scipy.integrate import quad f =lambda x: x**2 + (1/x**4) solution = quad(f, 1, 2) print("定积分的值：", solution) ``` >定积分的值： (2.625, 2.914335439641036e-14) $$\int_{-1}^{0} \frac{3x^4+3x^2+1}{x^2+1}dx$$。 提示：$$ (arctan x) \prime = \frac{3x^4+3x^2+1}{x^2+1}$$ ```python import sympy as sp # 定义变量和函数 x = sp.symbols('x') f = (3*x**4 + 3*x**2 + 1)/ (x**2 + 1) # 计算原函数 F = sp.integrate(f, x) # 计算在积分区间端点的原函数值 integral_value = F.subs(x, 0) - F.subs(x, -1) print("定积分的值：", integral_value.evalf()) print("当趋近于无穷：", sp.limit(f,x,sp.oo)) print("当趋近于负无穷时：", sp.limit(f,x,-sp.oo)) print("当趋近于0时：", sp.limit(f,x,0)) ``` >定积分的值： 1.78539816339745 当趋近于无穷： oo 当趋近于负无穷时： oo 当趋近于0时： 1 tn2>利用定积分的定义计算极限 $$\lim_{n\to \infty}\frac{1^p+2^p+..+n^p}{n^{p+1}}(p>0)$$ tn2>可以将其表示为以下定积分的极限形式： $$ \lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^{n} \left(\frac{k}{n}\right)^p $$ tn2>这个形式类似于定积分，其中被积函数是 \(x^p\)，积分区间是 \([0, 1]\)。所以，我们可以将这个极限表示为积分： $$ \lim_{n \to \infty} \frac{1^p + 2^p + .. + n^p}{n^{p+1}} =\lim_{n \to \infty} \frac{1}{n}\sum_{k=1}^{n}\left(\frac{k}{n}\right)^p = \int_{0}^{1} x^p $$ tn2>现在，我们可以计算这个积分的值： $$ \lim_{n \to \infty} \frac{1^p + 2^p + .. + n^p}{n^{p+1}} = \int_{0}^{1} x^p \,dx = \left[\frac{x^{p+1}}{p+1}\right]_{0}^{1} = \frac{1}{p+1} $$ tn2>因此，最终的极限为 $$ \frac{1}{p+1} $$。 ```python import sympy as sp # 定义符号和参数 n, p = sp.symbols('n p', positive=True, real=True) k = sp.symbols('k', integer=True) # 定义被积函数 f = (k/n)**p # 计算积分 integral_result = sp.integrate(f, (k, 1, n)) # 计算极限 limit_result = sp.limit(integral_result/n, n, sp.oo) # 打印结果 print("极限的结果：", limit_result) ``` >极限的结果： 1/(p + 1)