人工智能数学基础补习题(极限、无穷、导数、偏导数、梯度) 电脑版发表于:2023/11/30 17:38  >#人工智能数学基础补习题(极限、无穷、导数、偏导数、梯度) [TOC] ## SymPy 简单介绍 tn2>SymPy 是一个用于符号数学计算的 Python 库。符号数学计算是指在计算过程中保留符号表示,而不是进行数值逼近。SymPy 提供了一套丰富的功能,包括代数运算、微积分、方程求解、线性代数、解微分方程、级数展开、矩阵运算等计算。 ### 常用的SymPy内置符号 tn2>自然对数的底e的表达方式。 ```python import sympy as sp sp.E ``` >e tn2>求对数函数 ```python sp.log(sp.E) ``` >1 tn2>无穷大极限的表达方式`oo` ```python import sympy as sp 1/sp.oo ``` >0 tn2>圆周率 π 的表达方式 ```python sp.pi ``` tn2>对π的正弦函数 ```python sp.sin(sp.pi) ``` ### 用SymPy进行初等运算 | 函数 | 描述 | | ------------ | ------------ | | `sympy.log` | 求对数函数 | | `sympy.sin` | 正弦函数 | | `sympy.sqrt` | 求平方根函数 | | `sympy.root` | 求n次方根函数 | | `sympy.factorial` | 求阶乘函数 | ### 表达式与表达式求值 tn2>SymPy可以用一套符号系统来表示一个表达式,如函数、多项式等,并且可以进行求值。 ```python # 定义x为一个符号,表示一个变量 x = sp.Symbol('x') fx = 2*x+1 # fx 是一个表达式 fx.evalf(subs={x:2}) # 用evalf函数,传入变量的值,对表达式进行求值 ``` >5.0 ```python x,y = sp.symbols('x y') fx = 2*x+y fx.evalf(subs={x:1,y:2}) # 以字典的形式传入多个变量的值 # 如果只传入一个变量的值,则输出原来的表达式的值 ``` >4.0 ```python fx.evalf(subs={x:1}) ``` >y+2.0 ### 求极限用sympy.limit函数 $$\lim_{x\to \infty}\frac{\sin x}{x}$$ ```python import sympy from sympy import oo # 无穷是两个小写oo import numpy as np x=sympy.Symbol('x') f=sympy.sin(x)/x r=sympy.limit(f,x,oo) r ``` >0 $$\lim_{x\to 1}\frac{\ x^2-1}{x-1}$$ ```python import sympy from sympy import oo import numpy as np x=sympy.Symbol('x') f=(x**2-1)/(x-1) r=sympy.limit(f,x,1) r ``` >2 $$\lim_{x\to 0}\frac{\sin x}{3x-x^3}$$ ```python import sympy from sympy import oo import numpy as np x=sympy.Symbol('x') f=sympy.sin(x)/((3*x)+(x**3)) r=sympy.limit(f,x,0) r ``` >$$\frac{1}\{3}$$ ### 求导sympy.diff函数 tn2>求导的目的是找到一个函数在某一点的变化率,也就是函数在这一点的瞬时斜率。(单个因素) 求出下列函数的导数: $$y=\arcsin \sqrt{\sin x}$$ ```python from sympy import * from sympy.abc import x,y,z,f # diff求导函数,arcsin数学函数表示形式为asin diff(asin(sqrt(sin(x)))) ``` 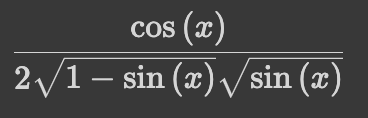 tn2>偏导数的目的是了解一个多变量函数在某个特定方向上的变化率。(多个因素) 求出下列表达式在点(1,2)处的偏导数。 $$f(x, y)=x^2+3xy+y^2$$ tn2>先获取x和y的偏导公式,再进行带入。 ```python from sympy import * from sympy.abc import x,y,z,f f=x**2+3*x*y+y**2 # 求对于x的导数 fx=diff(f,x) fx ``` >2x+3y ```python # 求对于y的导数 fy=diff(f,y) fy ``` >3x+2y ```python # 求在点(1,2)时,x的偏导数 fx.evalf(subs={x:1,y:2}) ``` >8.0 ```python # 求在点(1,2)时,y的偏导数 fy.evalf(subs={x:1,y:2}) ``` >7.0 ### 方向导数 tn2>在偏导数之上确定了沿生的方向。 梯度向量:包含了函数在该点对每个变量的偏导数(x,y,z)。 方向导数=?f(梯度向量)*v(方向向量) ### 梯度下降 tn2>梯度就是方向导数取最大值,就是下坡最近的一种方式。 实现下列梯度下降求解下面函数的最小值 $$min f(x)=x-y+2x^2+2xy+y^2$$ tn2>通过对x和y的偏导得知公式为 $$\frac{\partial f}{\partial x}=4*x+2*y+1$$ $$\frac{\partial f}{\partial y}=-1+2*x+2*y$$ tn>再此之前请确保安装了`ipympl`包。 ```python !pip install ipympl %matplotlib widget ``` ```python # 开启colab渲染,如果不是使用的google colab没有必要 from google.colab import output output.enable_custom_widget_manager() ``` ```python import matplotlib.pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D # 定义梯度函数 def Fun(x,y): return x - y + 2 * x * x + 2 * x * y + y * y # 求偏导x def PxFun(x,y): return 1 + 4 * x + 2 * y # 求偏导y def PyFun(x,y): return -1 + 2 * x + 2 * y fig = plt.figure() ax = plt.axes(projection='3d') # 取样并作满射联合 X,Y = np.mgrid[-2:2:40j, -2:2:40j] # 取样并作满射联合 Z = Fun(X,Y) # X,Y,Z 指定行和列 表面图上色 ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none') # 取样并作满射联合 ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') # 梯度下降 # 取步长 step = 0.0008 x = 0 y = 0 tag_x = [x] tag_y = [y] tag_z = [Fun(x,y)] # 3个坐标分别打入表中,该表用于绘制点 new_x = x new_y = y Over = False while Over == False: # 获取偏导并乘以阿尔法下降速度 new_x -= step * PxFun(x,y) new_y -= step * PyFun(x,y) if Fun(x,y) - Fun(new_x,new_y) < 7e-9: Over = True x = new_x y = new_y # 添加更新的点 tag_x.append(x) tag_y.append(y) tag_z.append(Fun(x,y)) ax.plot(tag_x,tag_y,tag_z,'r') plt.title('(x,y)-('+str(x)+','+str(y)+')') plt.show() ``` 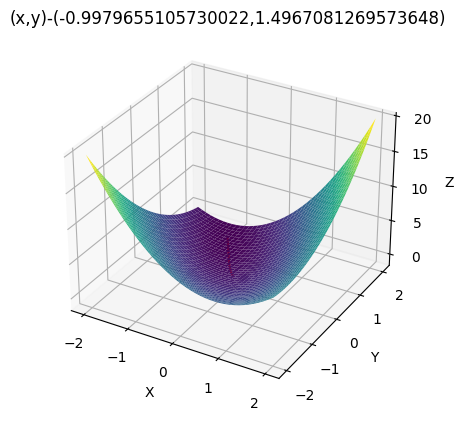 tn2>这里小于`7e-9`保证精度够小。 ```python # 输出最小的x,y,z x,y,Fun(x,y) ``` >(-0.9979655105730022, 1.4967081269573648, -1.2499942798392145) ## NumPy库简单介绍 tn2>NumPy(Numerical Python的缩写)是Python中用于科学计算的核心库之一。它提供了一个强大的多维数组对象(numpy.array)和用于处理这些数组的各种函数。NumPy是很多其他科学计算库的基础,包括Pandas、SciPy、Matplotlib等。 ### 数组的操作 ```python import numpy as np a = np.array([1,2,3]) # 创建一个rank的数组 print(a[0],a[1],a[2]) ``` >1 2 3 ```python b = np.array([[1,2,3],[4,5,6]]) print(b[0,0],b[0,1],b[0,2]) ``` >1 2 3 tn2>在绘制三维图表时,需要用到NumPy中的mgrid函数。 它会返回一个密集的多维网格,一般形式为`np.mgrid[start:end:step]` `start`:开始值 `end`:结束坐标 `step`:表示步数 ```python np.mgrid[-1:4:2] ``` >array([-1, 1, 3]) ```python np.mgrid[-1:4:2,-3:1:1] ``` 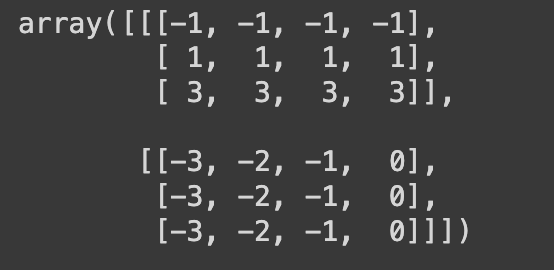 ## SciPy库简单介绍 tn2>SciPy是建立在NumPy基础上的一个开源科学计算库,提供了许多在科学和工程中常用的高级数学、信号处理、优化、统计等算法和工具。 ### 使用SciPy求导 tn2>使用`scipy.misc`模块下的`derivative`函数。 求f(x)在x0处的导数即f`(x0) ```python import numpy as np from scipy.misc import derivative def f(x): # 定义函数 return x**5 print(derivative(f, 2, dx=1e-6)) # 对函数在x=2处求导 ``` >80.00000000230045 tn>`dx`参数表示用于计算数值导数的微小变化量 tn2>使用`polyld()`函数构造`f(x)`,`polyld`函数的形参是多项式的系数,最左侧的是最高次数的系数,构造的函数为多项式。 Numpy的`polylder`函数和`deriv`函数的作用差不多,都是对多项式求导,可以得到函数导数的表达式和在某点的导数。 对下面的多项式进行求导 $$x^5+2x^4+3x^2+5$$  ```python # 对多项式x^5 + 2x^4 + 3x^2 + 5求导 import numpy as np p = np.poly1d([1,2,0,3,0,5]) # 通过系数构造多项式 print(p) ``` > 5 4 2 1 x + 2 x + 3 x + 5 ```python print(np.polyder(p,1)) # 求一阶导数 ``` > 4 3 5 x + 8 x + 6 x ```python print(np.polyder(p,1)(1.0)) # 求一阶导数在点x=1处的值 ``` >19.0 ```python print(p.deriv(1)) # 求一阶导数 ``` > 4 3 5 x + 8 x + 6 x ```python print(p.deriv(1)(1.0)) # 求一阶导数在点x=1处的值 ``` >19.0 ## 练习 tn2>求下列极限 $$\lim_{x\to 1}\sin (ln x)$$ ```python import sympy as sp x = sp.symbols('x') fx = sp.sin(sp.ln(x)) sp.limit(fx,x,1) ``` >0 $$\lim_{x\to 8}\frac{ 2^{1/3} - 2} {x-8}$$ ```python import sympy as sp x = sp.symbols('x') fx = (x**(1/3)-2)/(x-8) sp.limit(fx,x,8) ``` >$$\frac{1} {12}$$ tn2>求下列导数 $$y=x^4-2x^3+5sinx+ln3$$ ```python import sympy as sp x,y = sp.symbols('x y') y = x**4-2*x**3+5*sp.sin(x)+sp.ln(3) sp.diff(y,x) ``` 已知 $$z=(3x^2+y^2)^{4x+2y}$$,求在点(1,2)处的偏导数,并使用python编程(提示:复合函数求导,设$$u=3x^2+y^2$$ 、 $$v=4x+2y$$) ```python import sympy as sp z,x,y = sp.symbols('z x y') z = (3*x**2+y**2)**(4*x+2*y) # 对x求偏导 fx = sp.diff(z,x) fy = sp.diff(z,y) result_at_point = { 'dz/dx': fx.evalf(subs={x:1,y:2}), 'dz/dy': fy.evalf(subs={x:1,y:2}) } print("在点 (1, 2) 处的偏导数:", result_at_point) ``` >在点 (1, 2) 处的偏导数: {'dz/dx': 84401203.0927369, 'dz/dy': 48788945.5463684} 求函数 $$z=x^2+y^2$$ 在点`(1,2)`处沿点`(1,2)`到点$$(2,2+3^{1/2})$$方向的方向导数,以及在点(1,2)的梯度。 ```python import sympy as sp z,x,y = sp.symbols('z x y') z = x**2+y**2 # 对x求偏导 fx = sp.diff(z,x) fy = sp.diff(z,y) # 定义点 (1, 2) point_1_2 = sp.Point(1, 2) # 定义点 (2, 2 + sqrt(3)) point_2_2_sqrt3 = sp.Point(2, 2 + sp.sqrt(3)) # 计算从点 (1, 2) 到点 (2, 2 + sqrt(3)) 的方向向量 direction_vector = point_2_2_sqrt3 - point_1_2 # 计算方向导数 directional_derivative = sp.diff(z, x) * direction_vector[0] + sp.diff(z, y) * direction_vector[1] r1 =[fx.subs({x: 1, y: 2}),fy.subs({x: 1, y: 2})]; result_at_point = { '在点 (1, 2) 处的梯度': r1, # 使用subs也可以 "从点 (1, 2) 沿着到点 (2, 2 + sqrt(3)) 的方向的方向导数:": directional_derivative } print(":", result_at_point) ``` >{ '在点 (1, 2) 处的梯度': [2, 4], '从点 (1, 2) 沿着到点 (2, 2 + sqrt(3)) 的方向的方向导数:': 2*x + 2*sqrt(3)*y }