>#python 卷积图像识别实战 [TOC] 前提回顾 ------------ tn2>我们通过卷积将原始图像，通过卷积核，得出卷积后的图像，这个中间的过程被称为卷积层，最后纳入神经网络中进行训练。 当然你可能有这样的疑惑，就是如何得出卷积核的值呢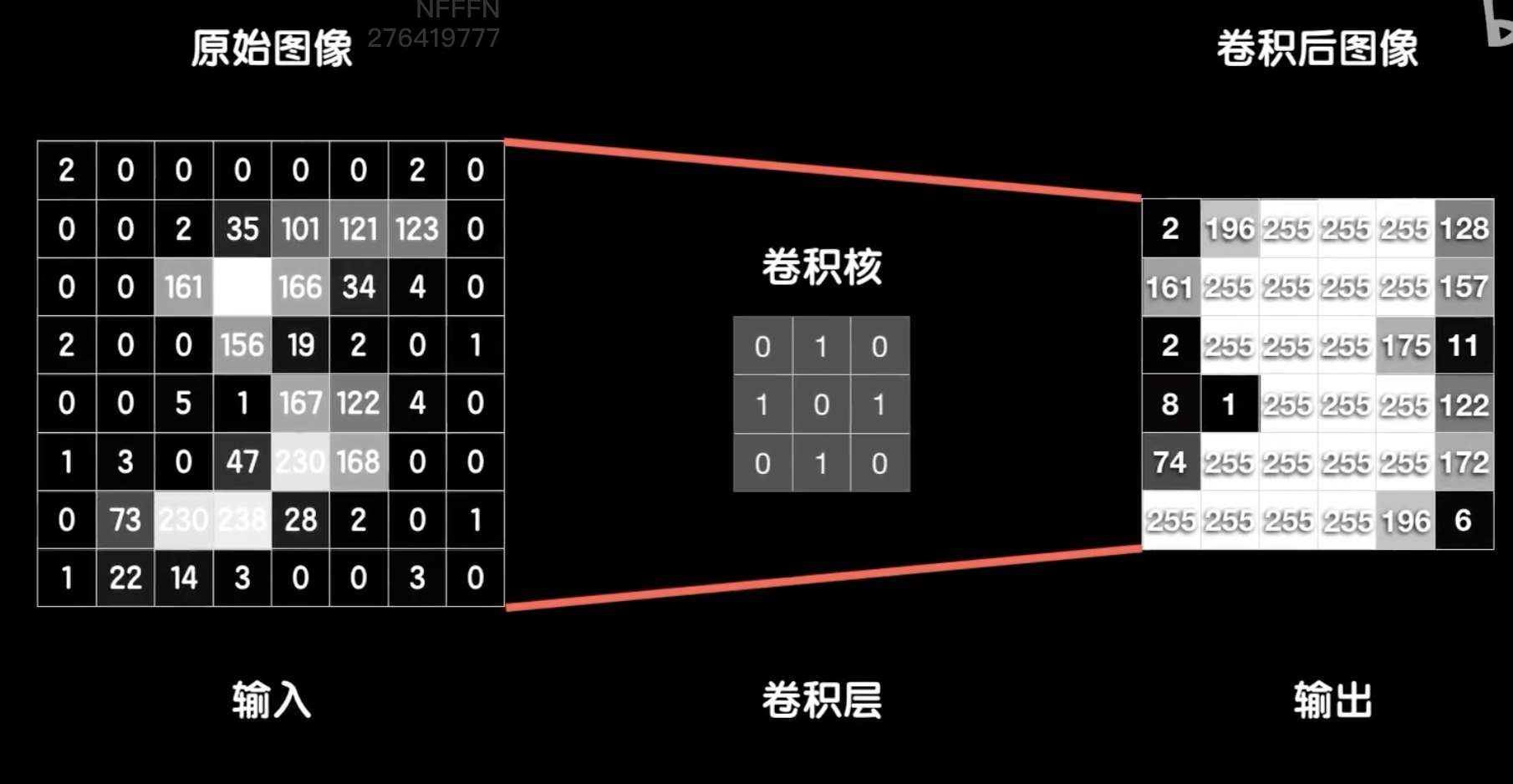？  tn2>卷积核的值是通过训练而来的。 还是与以前一样通过反向传播、梯度下降得来的，区别在于提取数据的方式不同。 卷积核值原理 ------------ tn2>假设我们的原始图的大小只有`4*4`，用一个`3*3`的卷积核去卷它，得到一个`2*2`的矩阵，卷完以后我们送入到一个全连接层中。 然后通过代价函数，把误差代价传播到这两层的各个权值和偏置项中，但如何传到这个卷积层中呢？貌似就不行了。 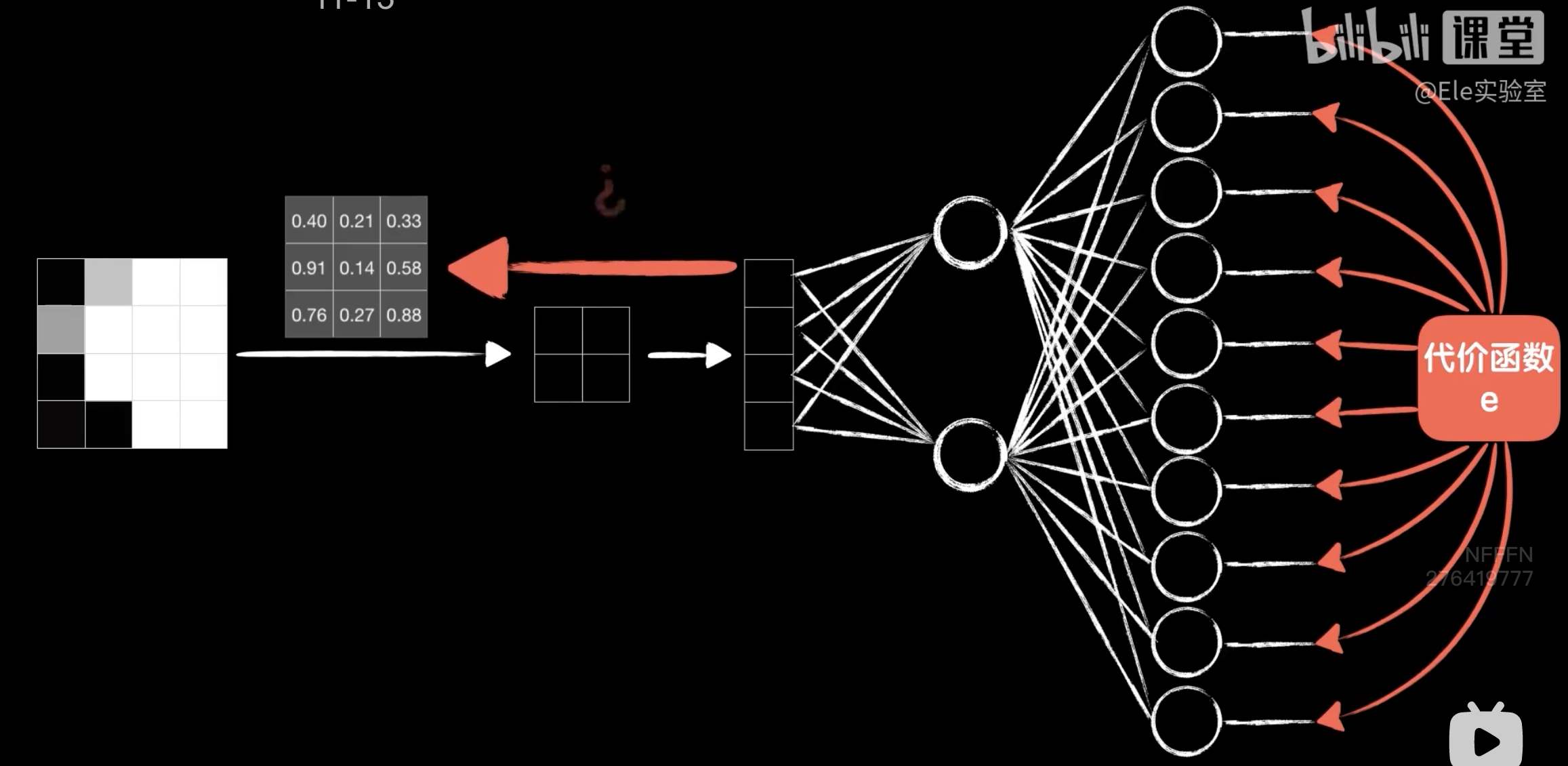 tn2>我们首先通过一个随机的`3*3`的卷积核，在`4*4`的原始图中得出`2*2`的卷积图像。然后把这四个值当成一个四个神经元，并加上偏置项b中，并再带上Rule函数就与神经网络没什么两样了。   tn2>但是这里面的细节还是有些不一样，首先这四个神经元的输出是根据卷积的过程排列而成的二位结构，而不是这样的平铺，到后面我们送到全链接层的时候我们需要手动把它平铺开；然后这四个神经元的输入并不相同，实际上是同一个图片的不同位置，并且使用同一个卷积核，所以他们的偏置项是一样的（这也是所谓的`参数共享`）。   tn2>一个卷积核提取出来的结果是提取图像的一种特征，我们需要提取图像更多的特征。 实际上你想要多少个特征你就搞多少个卷积核就好了。  tn2>而这三个卷积核得出的结果是一个三维向量，我们可以将三维的向量铺开就是一个一维的向量，然后在后面构造全链接层。  tn2>但在我们卷全连接之前我们还可不可以继续卷这个`6*6*3`的数据呢？当然可以比如LeNet-5网络。 LeNet-5神经网络结构 ------------ tn2>LeNet-5网络中就卷了两次之后再送入全连接层，那我们怎么去卷这个`6*6*3`的三维数据呢？实际上卷积运算不仅可以在二维上进行，同样可以在3维数据上进行，我们在3维数据上我们用3维的卷积核。  tn2>3维卷积的方式和二维几乎一模一样，三维卷积先找到数据和卷积核立方块对应的位置的元素相乘，然后加起来得到一个结果，当然最后还需要给结果加上偏置项b，再经过激活做非线性运算得到最后的输出。  tn2>当然我们也可以添加4个神经元变成`4*4*4`的张量数据，被卷积核的数据的第3个维度也就是所谓的通道数（`6*6*3`）。为什么是通道数？  tn2>如果我们的图像是彩色的RGP三个通道，那我们的输入是一个3通道的图像，所以把数据的第三个维度值称为通道数量，要对这样的值进行卷积那么卷积核也必须是三维的，而且第三个维度值也必须和数据的通道数一样。  tn2>如果我们还想把第二层卷积的输出结果继续卷，卷积核的第三个维度值需要和数据的通道数一样，我们可以使用`3*3*4`的卷积核。  tn2>除了我们两个卷积层以外还多出了两个立方块，这两个立方块就是所谓的池化层。  tn2>我们从输出的左上角开始框出`2*2`（举例不一定非得`2*2`）,再求出这个`2*2`数据的平均值得到第二个结果，然后一直顶到最右边。这个操作就是`池化`。  tn2>还有一种常见的方法是取最大值，就是取4个数的最大值，就叫最大池化，前面采用平均值的方式也叫AveragePooling平均池化。 图片卷积变大变小公式 ------------ tn2>变小公式，举例把`32*32`的图片像素转成`28*28`图片像素需要一个`5*5`的卷积核。 填充完了之后信息损失越来越多，之后人们又提出了新的填充方案。  tn2>比如卷积核是`5*5`就填充两圈，这样原始图片就从`28*28`填充成了`32*32`，这种卷积模式就是`Same模式`。  tn2>除了Same模式还有一种valid模式，越卷越小。  编程实践 ------------ tn2>模拟LeNet-5神经网络的实现。  ```python from keras.datasets import mnist import numpy as np from keras.models import Sequential from keras.layers import Dense from keras.optimizers import SGD import plot_utils_2 import matplotlib.pyplot as plt from keras.utils.np_utils import to_categorical # 导入二维卷积层 from keras.layers import Conv2D # 导入池化层 from keras.layers import AveragePooling2D # 平铺数组 from keras.layers import Flatten (X_train, Y_train), (X_test, Y_test) = mnist.load_data() # ndarray 的 reshape函数改变数组的形状。 # 把28*28的图片像素。 # 除以255的目的在于降低梯度下降的复杂度 # 训练集 X_train = X_train.reshape(60000,28,28,1)/255 # 测试集 X_test = X_test.reshape(10000,28,28,1)/255 # 转换成One Hot编码 Y_train = to_categorical(Y_train,10) Y_test = to_categorical(Y_test,10) model = Sequential() # filter 卷积核/过滤器数量 # kernel_size 卷积核尺寸 # strides 步长（一般都是挪动一步，当然也可以挪动多步） # input_shape 输入形状（这里是一个28*28*1的张量） # padding 填充模式 valid模式越小 # activation 激活函数 relu # # Convolutions model.add(Conv2D(filter=6,kernel_size=(5,5),strides=(1,1),input_shape=(28,28,1),padding='valid',activation='relu')) # 池化大小和窗口大小。 # 注意：keras中池化操作的步长不指定默认和pool_size一样，这里的步长也就默认是(2,2) # # Subsamping model.add(AveragePooling2D(pool_size=(2,2))) # 卷积出8*8*16 # # Convolutions model.add(Conv2D(filter=16,kernel_size=(5,5),strides=(1,1),padding='valid',activation='relu')) # 输出4*4*16 # # Subsamping model.add(AveragePooling2D(pool_size=(2,2))) # Full connection 平铺 model.add(Flatten()) # 输出层 model.add(Dense(units=120, activation='relu')) model.add(Dense(units=84, activation='relu')) model.add(Dense(units=10, activation='softmax')) # 送入训练 model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=0.05),metrics=['accuracy']) model.fit(X_train,Y_train,epochs=5000,batch_size=4096) # 评估测试集 # 添加测试数据进行测试模型的泛化能力 loss, accuracy = model.evaluate(X_test, Y_test) # 打印出损失和准确率 print("loss"+str(loss)) print("loss"+str(accuracy)) ```