>#python 矩阵、向量与Keras框架 [TOC] 矩阵、向量 ------------ tn2>随着传入的参数值越来越多，我们一步一步的写显得很麻烦，这时我们可以通过矩阵和向量来简化这一步骤。 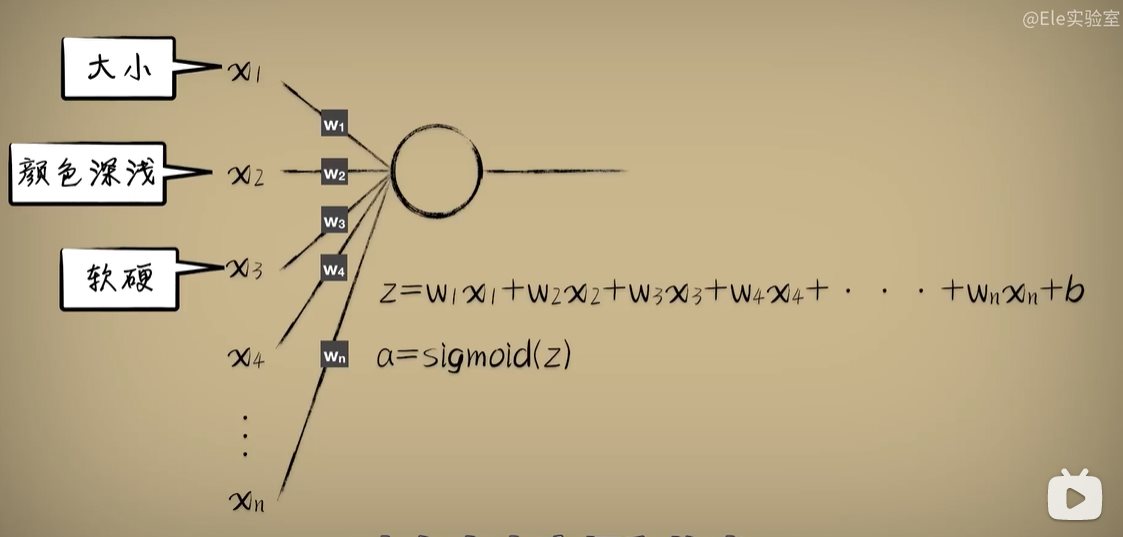 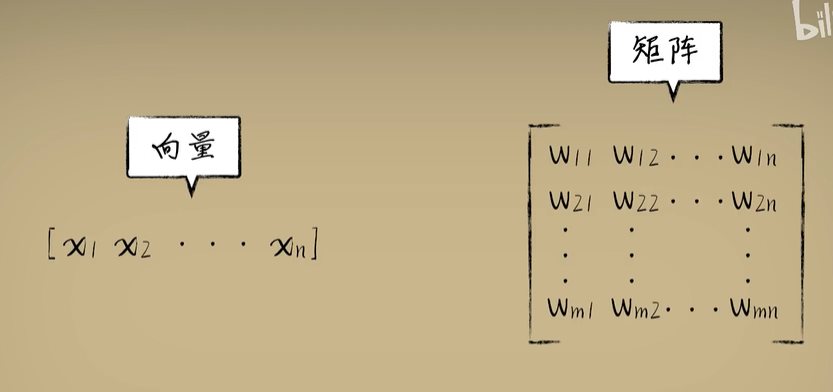 ### 矩阵与向量的诞生 tn2>以前我们学习数学的时候，一元一次函数，二元一次函数，三元一次函数。。。到n元一次函数，不够优雅也不够方便。 因此我们向量和矩阵诞生了。 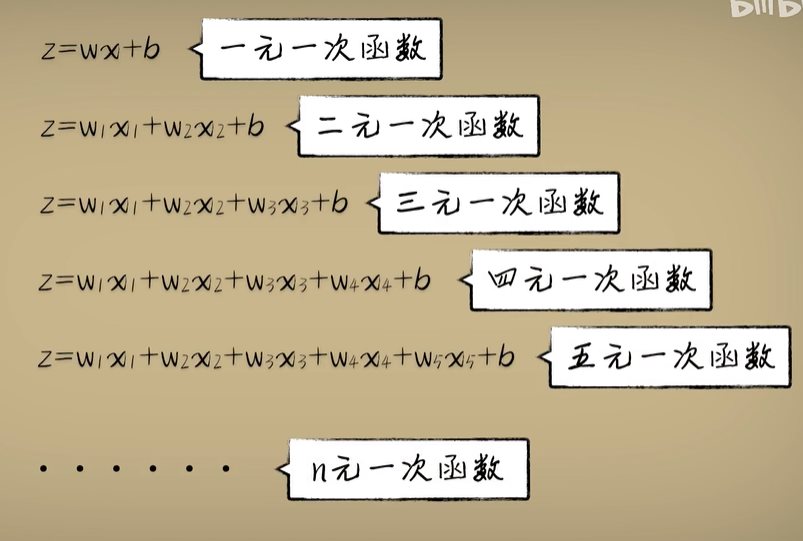 tn2>我们以三元一次函数举例，把自变量x1、x2、x3放到X中，把权重系数w1、w2、w3放入到另一个W向量中，把偏置项b也放入一个B向量中。 接着我们将W进行转置，将横着的W变成竖着的一列。 再将X与W^T进行相乘再相加，再加上偏置项B，这个计算的结果恰好就是我们函数的运算结果。  | 向量名 | 描述 | | ------------ | ------------ | | Z | 结果向量 | | X | 输入向量 | | W^T | 权重系数向量 | | B | 偏置系数向量 | tn2>这样做变得很简洁、很统一。 当我们加入两个隐藏层神经元的神经网络，输入实际上就是分别送入两个线性函数进行计算，这时候单靠向量视乎不行了，得用上矩阵才行。 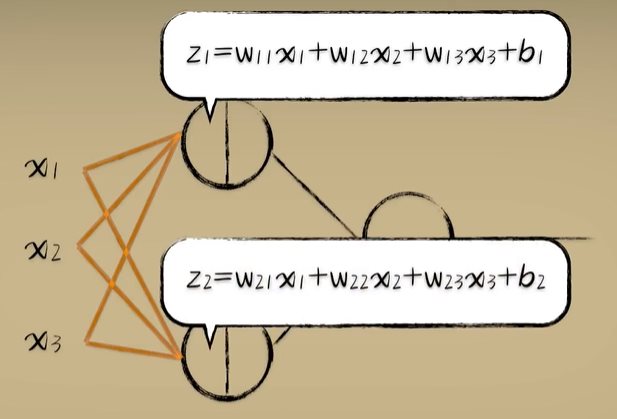 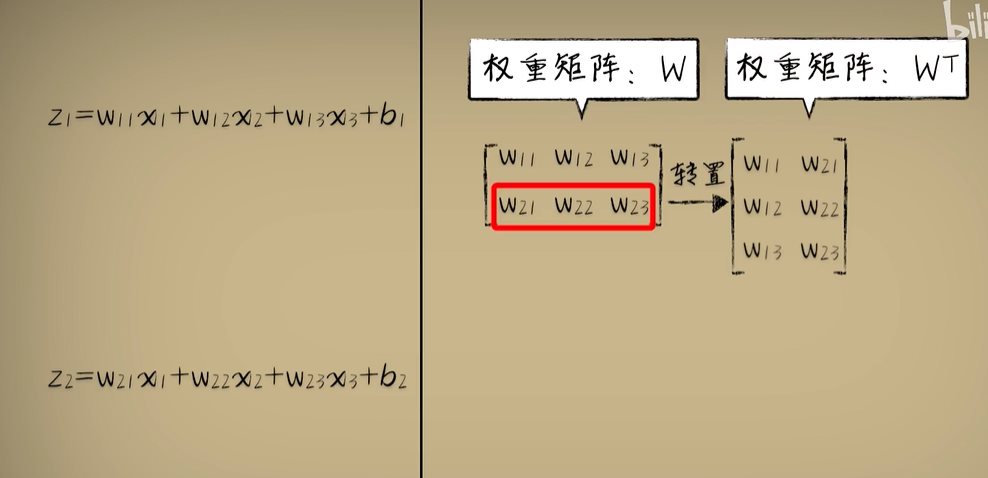 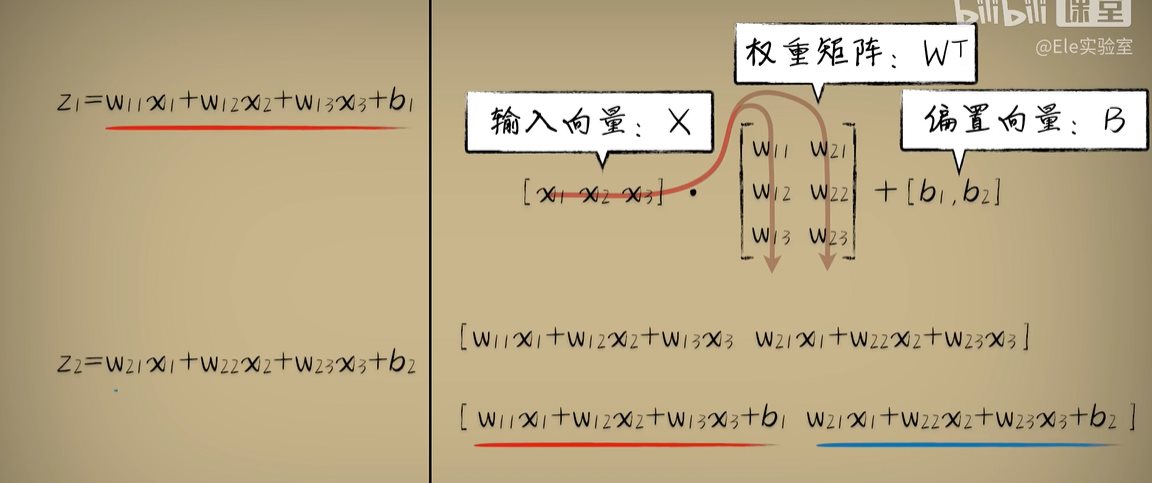 ### 编程实践 tn2>为了确保我们工具类的正常运行，我们先安装`tensorflow`和`keras`。 ```bash pip install tensorflow -i https://pypi.mirrors.ustc.edu.cn/simple/ pip install keras -i https://pypi.mirrors.ustc.edu.cn/simple/ ``` tn2>创建工具类`plot_utils_2.py`。 ```python import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D import numpy as np from keras.models import Sequential #导入keras def show_scatter_curve(X,Y,pres): plt.scatter(X, Y) plt.plot(X, pres) plt.show() def show_scatter(X,Y): if X.ndim>1: show_3d_scatter(X,Y) else: plt.scatter(X, Y) plt.show() def show_3d_scatter(X,Y): x = X[:,0] z = X[:,1] fig = plt.figure() ax = fig.add_subplot(111,projection='3d') ax.scatter(x, z, Y) plt.show() def show_surface(x,z,forward_propgation): x = np.arange(np.min(x),np.max(x),0.1) z = np.arange(np.min(z),np.max(z),0.1) x,z = np.meshgrid(x,z) y = forward_propgation(X) fig = plt.figure() ax = fig.add_subplot(111,projection='3d') ax.plot_surface(x, z, y, cmap='rainbow') plt.show() def show_scatter_surface(X,Y,forward_propgation): if type(forward_propgation) == Sequential: show_scatter_surface_with_model(X,Y,forward_propgation) return x = X[:,0] z = X[:,1] y = Y fig = plt.figure() ax = fig.add_subplot(111,projection='3d') ax.scatter(x, z, y) x = np.arange(np.min(x),np.max(x),0.1) z = np.arange(np.min(z),np.max(z),0.1) x,z = np.meshgrid(x,z) X = np.column_stack((x[0],z[0])) for j in range(z.shape[0]): if j == 0: continue X = np.vstack((X,np.column_stack((x[0],z[j])))) r = forward_propgation(X) y = r[0] if type(r) == np.ndarray: y = r y = np.array([y]) y = y.reshape(x.shape[0],z.shape[1]) ax.plot_surface(x, z, y, cmap='rainbow') plt.show() def show_scatter_surface_with_model(X,Y,model): #model.predict(X) x = X[:,0] z = X[:,1] y = Y fig = plt.figure() ax = fig.add_subplot(111,projection='3d') ax.scatter(x, z, y) x = np.arange(np.min(x),np.max(x),0.1) z = np.arange(np.min(z),np.max(z),0.1) x,z = np.meshgrid(x,z) X = np.column_stack((x[0],z[0])) for j in range(z.shape[0]): if j == 0: continue X = np.vstack((X,np.column_stack((x[0],z[j])))) y = model.predict(X) # return # y = model.predcit(X) y = np.array([y]) y = y.reshape(x.shape[0],z.shape[1]) ax.plot_surface(x, z, y, cmap='rainbow') plt.show() def pre(X,Y,model): model.predict(X) ``` tn2>更改上一节课的编码方式使用矩阵的方式来进行。 ```python import dataset import numpy as np import plot_utils_2 m = 100 # X,Y = dataset.get_beans7(m) print(X) print(Y) # 三维散点图 plot_utils_2.show_scatter(X,Y) # w1 = 0.1 # w2 = 0.1 # 改成向量 W = np.array([0.1,0.1]) # b = 0.1 B = np.array([0.1]) # 前向传播 def forward_propgation(X): # 预测函数 # z = w1 * x1s + w2 * x2s + b # 矩阵计算 Z = X.dot(W.T) + B # sigmoid函数求导 # a = 1/(1+np.exp(-z)) A = 1/(1+np.exp(-Z)) return A # 绘制一次求导的过程 plot_utils_2.show_scatter_surface(X,Y,forward_propgation) # 梯度下降 500 * 100 for _ in range(500): for i in range(m): Xi = X[i] Yi = Y[i] # 进行前向传播一次 A = forward_propgation(Xi) # 平方差 E = (Yi - A) ** 2 # e对a的求导 dEdA = -2*(Yi-A) # a对z的求导 dAdZ = A*(1-A) # z对w的求导 dZdW = Xi # z对b的求导 dZdB = 1 # 获取de对dw求导 dEdW = dEdA * dAdZ * dZdW # 获取de对db求导 dEdB = dEdA * dAdZ * dZdB # 设置阿尔法的弧度为0.01 alpha = 0.01 # 计算误差 W = W - alpha * dEdW B = B - alpha * dEdB plot_utils_2.show_scatter_surface(X,Y,forward_propgation) ``` 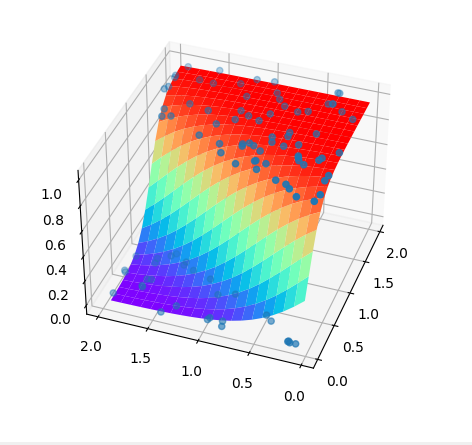 Keras机器学习框架 ------------ ### 什么是Keras？ tn2>Keras 是一个开源的深度学习框架，以 Python 语言编写，能够在 TensorFlow, CNTK 和 Theano 之上运行。Keras 是一个高层次的 API，可以方便快捷地构建和训练神经网络，专注于用户体验、模块化和可拓展性。它提供了一组简单易用的工具，可帮助用户定义神经网络的层、激活函数、损失函数、优化器、单元等等，并支持大量数据集的输入与输出操作。Keras 为深度学习的实验和快速原型工作提供了一个高效的开发环境。 Keras相当于Python语言简单易用，Tensorflow相当于C语言灵活强大。  tn2>我们自己实现一个神经元，首先需要前向传播，然后是代价函数、反向传播、梯度下降。 而Keras实现一个神经元只需要短短的五行代码。 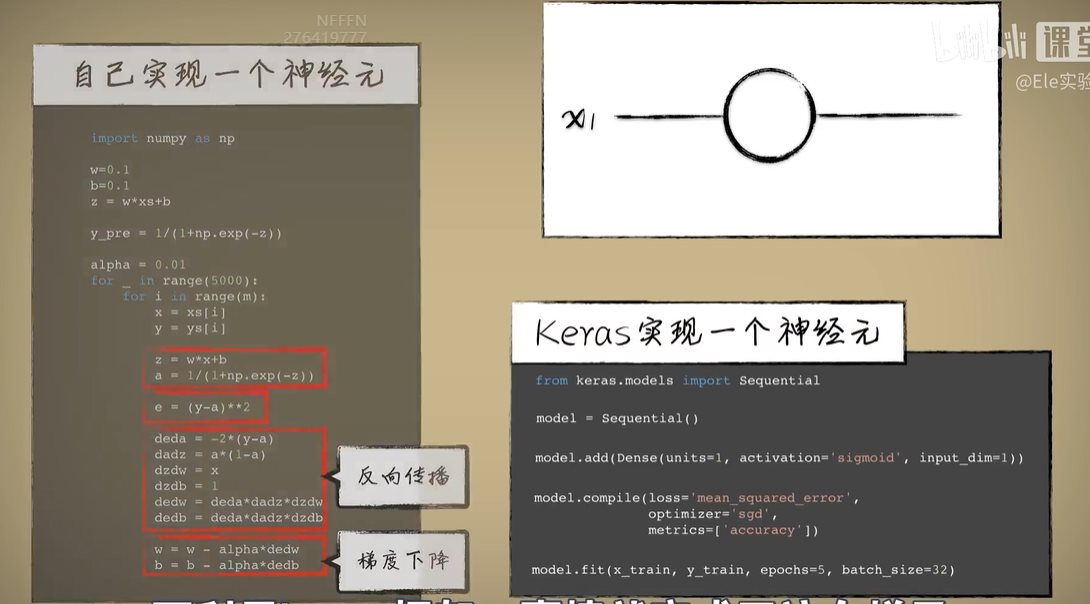 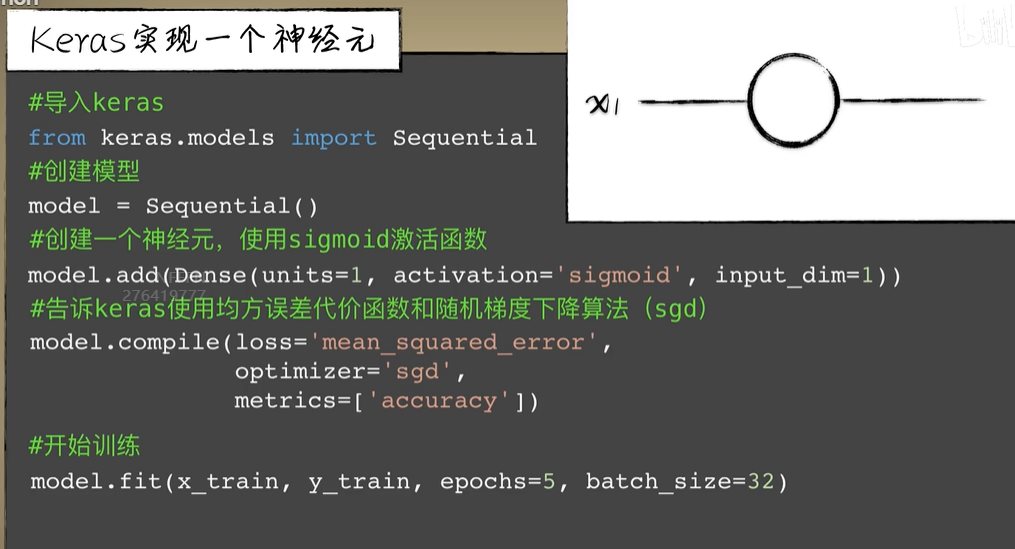 tn2>如果希望把神经元变成两个，可以把units=1变成units=2.  tn2>最后汇合一下神经元就可以加一个神经元。  ### Keras的缺点 tn2>Keras并不是一个独立的框架，它是基于Tensorflow、CNTK、Theano之上写的一个框架，可以理解为python语言与C语言，如下图所示。  tn2>高度集成的框架，会出现对细节把控的不到位。 ### 编程实践一 tn2>接下来我们通过Keras来实现四大模块。  tn2>首先我们解释一些名词。 Sequential这个实体可以理解为堆叠神经网络的载体。 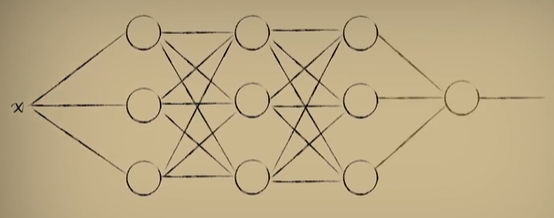 tn2>Dense表示一个全连接层，简单来讲两个神经元的隐藏层是一个Dense，单个神经元的输出也是一个Dense。全连接表示所有层都进行相互关联。 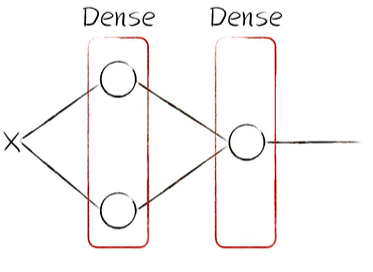 tn2>添加豆豆类`dataset.py`。 ```python import numpy as np def get_beans(counts): xs = np.random.rand(counts) xs = np.sort(xs) # ys = [1.2*x+np.random.rand()/10 for x in xs] ys = [(0.7*x+(0.5-np.random.rand())/5+0.5) for x in xs] return xs,ys def get_beans2(counts): xs = np.random.rand(counts) xs = np.sort(xs) ys = np.array([(0.7*x+(0.5-np.random.rand())/5+0.5) for x in xs]) return xs,ys def get_beans3(counts): xs = np.random.rand(counts)*2 xs = np.sort(xs) ys = np.zeros(counts) for i in range(counts): x = xs[i] yi = 0.7*x+(0.5-np.random.rand())/50+0.5 if yi > 0.8 and yi < 1.4: ys[i] = 1 return xs,ys def get_beans4(counts): xs = np.random.rand(counts,2)*2 ys = np.zeros(counts) for i in range(counts): x = xs[i] if (np.power(x[0]-1,2)+np.power(x[1]-0.3,2))<0.5: ys[i] = 1 return xs,ys def get_beans7(counts): xs = np.random.rand(counts,2)*2 ys = np.zeros(counts) for i in range(counts): x = xs[i] if (x[0]-0.5*x[1]-0.1)>0: ys[i] = 1 return xs,ys def get_beans0(counts): xs = np.random.rand(counts) xs = np.sort(xs) ys = np.zeros(counts) for i in range(counts): x = xs[i] yi = 0.7*x+(0.5-np.random.rand())/50+0.5 if yi > 0.8: ys[i] = 1 return xs,ys ``` tn2>编辑`keras_for_blue.py`代码 ```python import dataset import numpy as np import plot_utils_2 # Sequential 表示堆叠神经网络的序列 from keras.models import Sequential # 层与层之间都相互连接 from keras.layers import Dense m = 100 X,Y = dataset.get_beans0(m) plot_utils_2.show_scatter(X,Y) model = Sequential() # Dense 表示层 # units 当前层神经元数量 # sigmoid 激活函数类型 # input_dim 输入数据特征维度 dense = Dense(units=2,activation='sigmoid',input_dim=1) # 添加层 model.add(dense) # mean_squared_error 均方误差 # sgd 优化器 随机梯度下降算法 'sgd' 如果要设置阿尔法SGD(lr=0.05) # 评估标准 accuracy 准确度 model.compile(loss='mean_squared_error',optimizer='sgd',metrics=['accuracy']) # 10次训练，5000回合数 model.fit(X, Y, epochs=5000,batch_size=10) # 预测 pres = model.predict(X) # 同时绘制一下散点图和预测曲线 plot_utils_2.show_scatter_curve(X,Y,pres) ``` 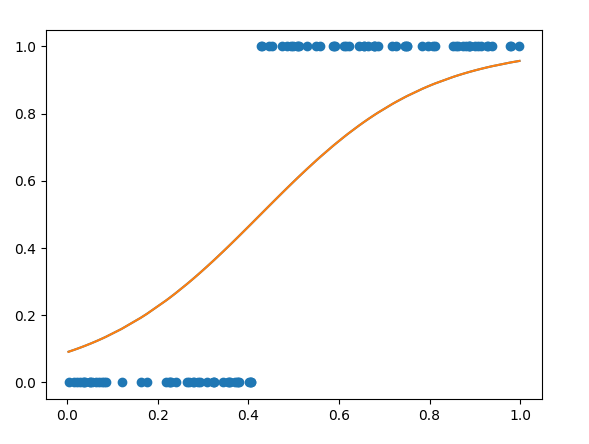 ### 编程实践二 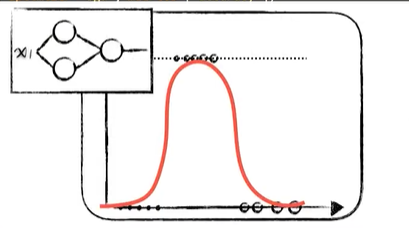 ```python import dataset import numpy as np import plot_utils_2 # Sequential 表示堆叠神经网络的序列 from keras.models import Sequential # 层与层之间都相互连接 from keras.layers import Dense from keras.optimizers import SGD m = 100 X,Y = dataset.get_beans3(m) plot_utils_2.show_scatter(X,Y) model = Sequential() # Dense 表示层 # units 当前层神经元数量 # sigmoid 激活函数类型 # input_dim 输入数据特征维度 dense = Dense(units=2,activation='sigmoid',input_dim=1) # 添加层 model.add(dense) # 添加层 model.add(Dense(units=1,activation='sigmoid')) # mean_squared_error 均方误差 # sgd 优化器 随机梯度下降算法 'sgd' 如果要设置阿尔法SGD(lr=0.05) # 评估标准 accuracy 准确度 model.compile(loss='mean_squared_error',optimizer=SGD(lr=0.05),metrics=['accuracy']) # 10次训练，5000回合数 model.fit(X, Y, epochs=5000,batch_size=10) # 预测 pres = model.predict(X) # 同时绘制一下散点图和预测曲线 plot_utils_2.show_scatter_curve(X,Y,pres) ```  ### 编程实践三  ```python import dataset import numpy as np import plot_utils_2 from keras.models import Sequential # 层与层之间都相互连接 from keras.layers import Dense from keras.optimizers import SGD m = 100 X,Y = dataset.get_beans7(m) plot_utils_2.show_scatter(X,Y) model = Sequential() # Dense 表示层 # units 当前层神经元数量 # sigmoid 激活函数类型 # input_dim 输入数据特征维度 dense = Dense(units=1,activation='sigmoid',input_dim=2) # 添加层 model.add(dense) # mean_squared_error 均方误差 # sgd 优化器 随机梯度下降算法 'sgd' 如果要设置阿尔法SGD(lr=0.05) # 评估标准 accuracy 准确度 model.compile(loss='mean_squared_error',optimizer=SGD(lr=0.05),metrics=['accuracy']) # 10次训练，5000回合数 model.fit(X, Y, epochs=5000,batch_size=10) # 预测 pres = model.predict(X) # 同时绘制一下散点图和预测曲线 plot_utils_2.show_scatter_surface(X,Y,model) ```  ### 编程实践四  ```python import dataset import numpy as np import plot_utils_2 from keras.models import Sequential # 层与层之间都相互连接 from keras.layers import Dense from keras.optimizers import SGD m = 100 X,Y = dataset.get_beans4(m) plot_utils_2.show_scatter(X,Y) model = Sequential() # Dense 表示层 # units 当前层神经元数量 # sigmoid 激活函数类型 # input_dim 输入数据特征维度 dense = Dense(units=2,activation='sigmoid',input_dim=2) # 添加层 model.add(dense) model.add(Dense(units=1,activation='sigmoid')) # mean_squared_error 均方误差 # sgd 优化器 随机梯度下降算法 'sgd' 如果要设置阿尔法SGD(lr=0.05) # 评估标准 accuracy 准确度 model.compile(loss='mean_squared_error',optimizer=SGD(lr=0.05),metrics=['accuracy']) # 10次训练，5000回合数 model.fit(X, Y, epochs=5000,batch_size=10) # 预测 pres = model.predict(X) # 同时绘制一下散点图和预测曲线 plot_utils_2.show_scatter_surface(X,Y,model) ```