>#python 高维空间:机器如何面对越来越复杂的问题(学习笔记) [TOC] 机器如何面对越来越复杂的问题？ ------------ tn2>当我们豆豆的毒性不仅与大小有关，还与颜色有关的时候我们就需要三维坐标系，来显示各不相同的豆豆和毒性的关系。 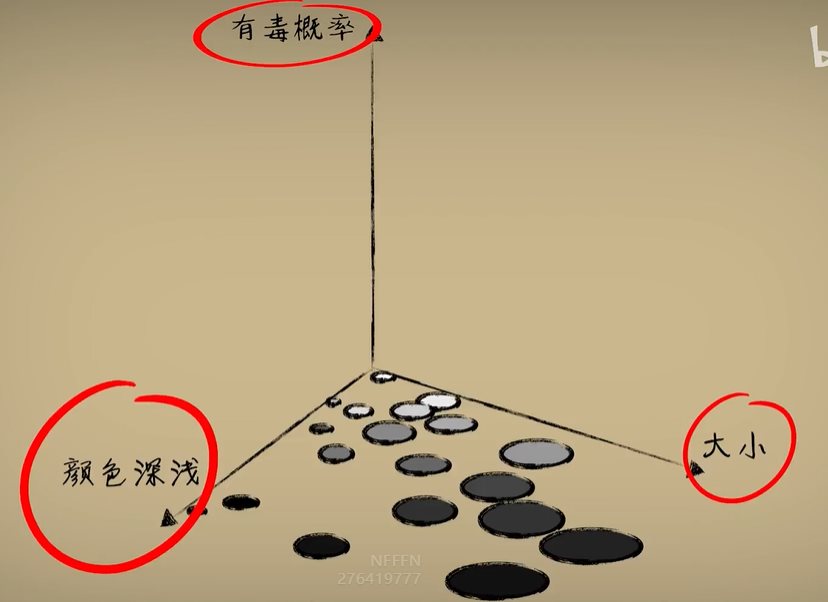 tn2>而只有满足某些大小和颜色深浅的豆豆才有毒，红色的豆豆有毒的概率是1，其他无毒的是0。 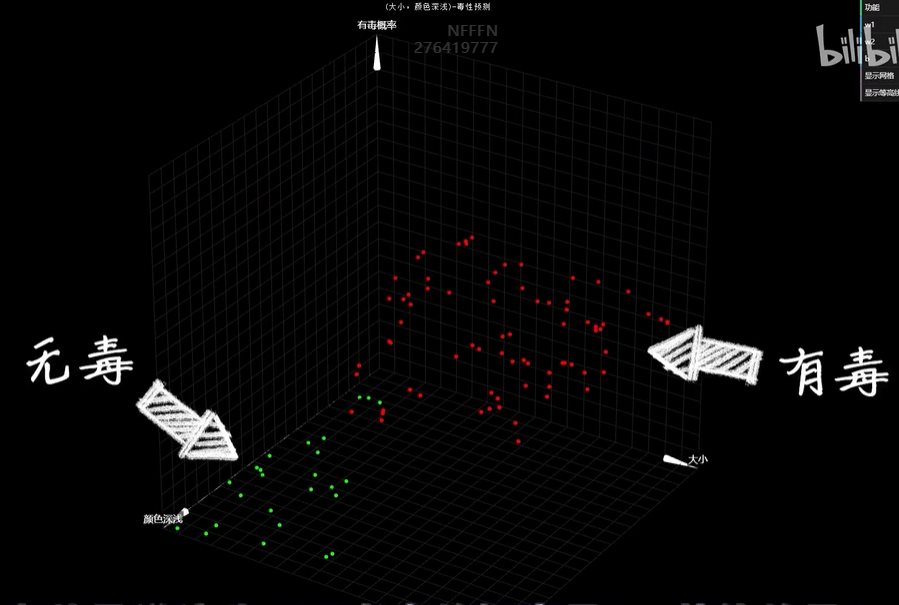 tn2>由于多了一项颜色的树突输入，预测函数的线性部分也从一元一次函数变成二元一次函数，这个函数通过三维画出来就是一个平面，再通过Sigmoid函数画出来就是一个曲面。 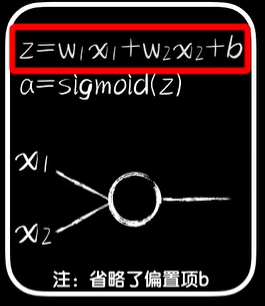   tn2>当我们找到预测曲面上预测值为0.5的点，连接在一起用地理里的概念来讲就是为0.5的等高线，连接起来是一条直线。 这条直线大于0.5表示有毒，小于0.5表示无毒。  tn2>当我们从上往下看俯视图效果的时候，这个0.5的等高线也就是**类型分割线**。  tn2>在之前的sigmoid中，也有等高线，只是在二维平面化成了一个点称为**等高点**。  tn2>通过不断调节权重参数w1，w2以及偏置项b，可以让预测模型的登高线顺利分割出有毒和无毒两类豆豆。  tn2>而当有毒的豆豆是一个曲面时，这时候就需要多个神经元来进行扭曲才行。  tn2>在三维空间中的等高线是一个曲线，而从二维的视角这两个点被称为直点。  tn2>当我们考虑的输入数据越多，特征维度就越多。  tn2>如果一个一个去写它们的表达式就太麻烦了，到后面我们可以使用向量和矩阵来进行计算。 编程实践 ------------ tn2>接下来的编程实验，我们将一个输入编程两个输入的神经元，豆豆预测的维度为二。  tn2>张量与数组的关系  tn2>首先我们导入豆豆的取值。 ```python import numpy as np def get_beans7(counts): xs = np.random.rand(counts,2)*2 ys = np.zeros(counts) for i in range(counts): x = xs[i] if (x[0]-0.5*x[1]-0.1)>0: ys[i] = 1 return xs,ys ``` tn2>然后添加绘图工具的代码`plot_utils.py` ```python import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D import numpy as np def show_scatter(xs,y): x = xs[:,0] z = xs[:,1] fig = plt.figure() # 创建3D对象 ax = fig.add_subplot(111,projection='3d') ax.scatter(x, z, y) plt.show() def show_surface(x,z,forward_propgation): x = np.arange(np.min(x),np.max(x),0.1) z = np.arange(np.min(z),np.max(z),0.1) x,z = np.meshgrid(x,z) y = forward_propgation(x,z) fig = plt.figure() ax = fig.add_subplot(111,projection='3d') ax.plot_surface(x, z, y, cmap='rainbow') plt.show() def show_scatter_surface(xs,y,forward_propgation): x = xs[:,0] z = xs[:,1] fig = plt.figure() ax = fig.add_subplot(111,projection='3d') ax.scatter(x, z, y) x = np.arange(np.min(x),np.max(x),0.01) z = np.arange(np.min(z),np.max(z),0.01) x,z = np.meshgrid(x,z) y = forward_propgation(x,z) ax.plot_surface(x, z, y, cmap='rainbow') plt.show() ``` tn2>先编写几行简单的代码，来生成豆豆，第一列是大小，第二列是颜色值。 ```python import dataset import numpy as np import plot_utils m = 100 xs,ys = dataset.get_beans7(m) print(xs) print(ys) ```  tn2>这个ys表示毒性，0表示无毒，1表示有毒。  tn2>接下来我们通过调用`plot_utils`类的`show_scatter`方法来绘制散点图。 ```python import dataset import numpy as np import plot_utils m = 100 xs,ys = dataset.get_beans7(m) print(xs) print(ys) # 三维散点图 plot_utils.show_scatter(xs,ys) ``` 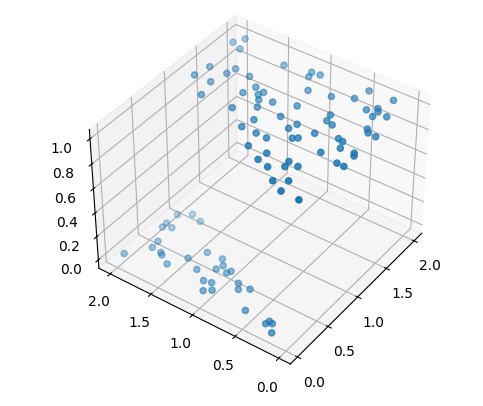 ```python w1 = 0.1 w2 = 0.1 b = 0.1 # 大小 x1s = xs[:,0] # 深浅 x2s = xs[:,1] # 前向传播 def forward_propgation(x1s,x2s): # 预测函数 z = w1 * x1s + w2 * x2s + b # sigmoid函数求导 a = 1/(1+np.exp(-z)) return a # 绘制一次求导的过程 plot_utils.show_scatter_surface(xs,ys,forward_propgation) ``` 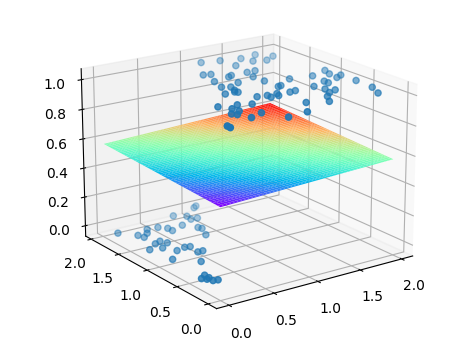 ```python import dataset import numpy as np import plot_utils m = 100 xs,ys = dataset.get_beans7(m) print(xs) print(ys) # 三维散点图 plot_utils.show_scatter(xs,ys) w1 = 0.1 w2 = 0.1 b = 0.1 # 大小 x1s = xs[:,0] # 深浅 x2s = xs[:,1] # 前向传播 def forward_propgation(x1s,x2s): # 预测函数 z = w1 * x1s + w2 * x2s + b # sigmoid函数求导 a = 1/(1+np.exp(-z)) return a # 绘制一次求导的过程 plot_utils.show_scatter_surface(xs,ys,forward_propgation) # 梯度下降 500 * 100 for _ in range(500): for i in range(m): x = xs[i] y = ys[i] # 单个大小 x1 = x[0] # 单个颜色值 x2 = x[1] # 进行前向传播一次 a = forward_propgation(x1,x2) # 平方差 e = (y - a) ** 2 # e对a的求导 deda = -2*(y-a) # a对z的求导 dadz = a*(1-a) # z对w1的求导 dzdw1 = x1 # z对w2的求导 dzdw2 = x2 # z对b的求导 dzdb = 1 # 获取de对dw1求导 dedw1 = deda * dadz * dzdw1 # 获取de对dw2求导 dedw2 = deda * dadz * dzdw2 # 获取de对db求导 dedb = deda * dadz * dzdb # 设置阿尔法的弧度为0.01 alpha = 0.01 # 计算误差 w1 = w1 - alpha * dedw1 w2 = w2 - alpha * dedw2 b = b - alpha * dedb # 绘制 plot_utils.show_scatter_surface(xs,ys,forward_propgation) ```