>#python 神经网络隐藏层学习笔记 [TOC] 回顾上节 ------------ tn2>关于我们对与豆豆的分类毒性，我们可以使用Logistic函数对豆豆的毒性进行分类，但是如果豆豆大到一定的程度它没有毒性了那么单一的Logistic函数就没啥用了，如下图所示。  tn2>单个的不行，我们可以使用多个Logistic函数来解决这个问题。 像这样：  tn2>这个时候我们就需要将第一个神经元（x+偏置项b1_1），通过线性函数的计算再通过激活函数得到最终的输出,再利用梯度下降算法得出Logistic函数的样子。 第二个神经元同样如此（x+偏置项b2_1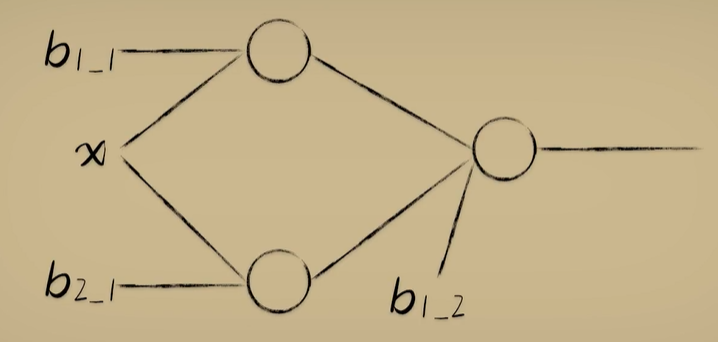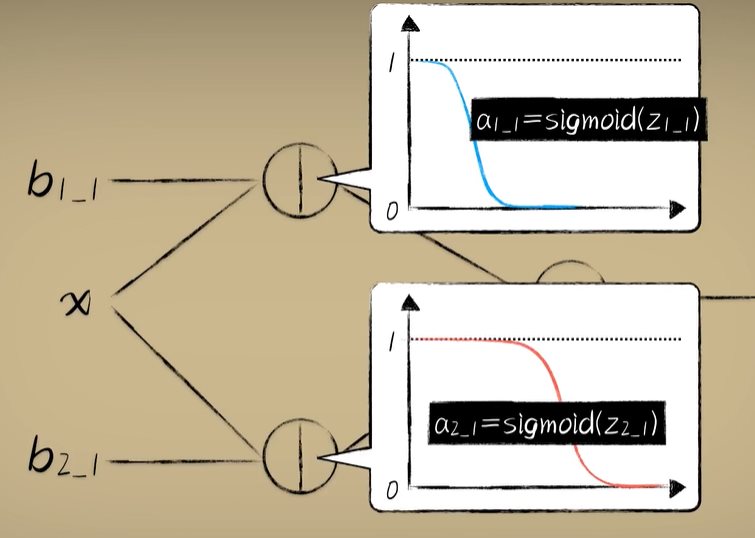）。   tn2>把这两个的输出作为第三个神经元的输入（x+偏置项b1_2）,求和之后会得出这样的值，再通过梯度下降这就是我们想要的结果。 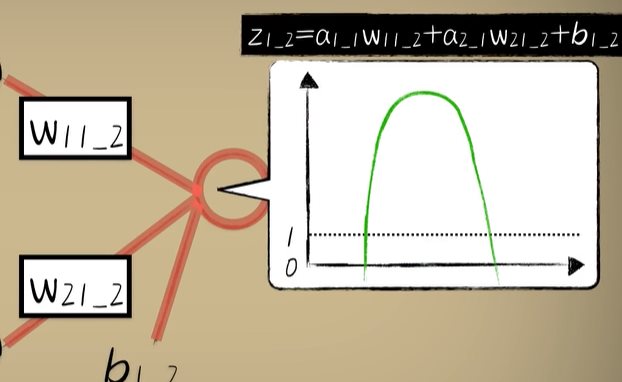 什么是隐藏层？ ------------ tn2>举例：当我们输入到不同的维度（神经元）中每个维度通过不断的调整权重进行激活，得出不一样的结果最后再进行合并降维得到输出。通过输入的更多抽象维度产生更多的解读而实现更加复杂的分类效果，而中间这些新添加的神经元节点也称为`隐藏层`。 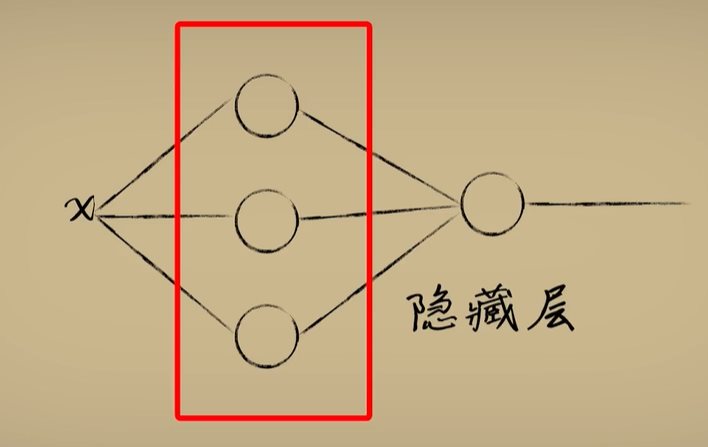 tn2>显而易见的是隐藏层越多思考得就越复杂，计算量也就随之越来越大。 到后面我们还会添加纵向的神经元添加更深的隐藏层。  tn2>当我们的神经层有三个以上，就被称之为深度网络模型。  代码实践 ------------ tn2>豆豆毒性生成。 ```python import numpy as np def get_beans3(counts): xs = np.random.rand(counts)*2 xs = np.sort(xs) ys = np.zeros(counts) for i in range(counts): x = xs[i] yi = 0.7*x+(0.5-np.random.rand())/50+0.5 if yi > 0.8 and yi < 1.4: ys[i] = 1 return xs,ys ```  ```python import dataset import matplotlib.pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D m = 100 # 获取100个豆豆 xs,ys = dataset.get_beans3(m) plt.title("Size-Toxicity Function",fontsize=12) plt.xlabel("Bean Size") plt.ylabel("Toxicity") plt.scatter(xs,ys) # sigmoid 函数 1/(1+e^-x) def sigmoid(x): return 1/(1+np.exp(-x)) # 第一层 # 第一个神经元 使用随机数 w11_1 = np.random.rand() b1_1 = np.random.rand() # 第二个神经元 w12_1 = np.random.rand() b2_1 = np.random.rand() # 第二层 # 第一个神经元 w11_2 = np.random.rand() w21_2 = np.random.rand() b2_2 = np.random.rand() b1_2 = np.random.rand() def forward_propgation(xs): # 前向传播 # 使用函数进行前向传播过程。 # 第一层第一个求出预测值 z1_1 = w11_1 * xs + b1_1 a1_1 = sigmoid(z1_1) # 第一层第二个求出预测值 z2_1 = w12_1 * xs + b2_1 a2_1 = sigmoid(z2_1) # 第二层第一个求出预测值 z1_2 = w11_2 * a1_1 + w21_2 * a2_1 + b1_2 a1_2 = sigmoid(z1_2) return a1_2,z1_2,a2_1,z2_1,a1_1,z1_1 a1_2,z1_2,a2_1,z2_1,a1_1,z1_1 = forward_propgation(xs) plt.plot(xs,a1_2) plt.show() for _ in range(5000): for i in range(100): # 获取散点的值 x = xs[i] y = ys[i] # 首先获取前向传播获取结果 ,输入单个样本 a1_2,z1_2,a2_1,z2_1,a1_1,z1_1 = forward_propgation(x) # 反向传播（求导） # 误差代价函数e e = (y - a1_2)**2 # 第二层第一个 # e对a1_2的求导 de/da = -2(y-a) deda1_2 = -2*(y-a1_2) # a1_2对z1_2的求导 da/dz = a(1-a) da1_2dz1_2 = a1_2*(1-a1_2) # dz/dw的求导，过程是这样的z = wx + b，那么x就是它导数 # 举例：dz1_2dw11_2 = w11_2a1_1 + b1_2 = a1_1 dz1_2dw11_2 = a1_1 dz1_2dw21_2 = a2_1 # de/dw的求导，de/da * da/dz * dz/dw = de/dw dedw11_2 = deda1_2 * da1_2dz1_2 * dz1_2dw11_2 dedw21_2 = deda1_2 * da1_2dz1_2 * dz1_2dw21_2 # dz/db的求导 z = wx + b，一介函数dz/db的求导为1 dz1_2db1_2 = 1 # de/db的求导 de/da * da/dz * dz/db = de/db dedb1_2 = deda1_2 * da1_2dz1_2 * dz1_2db1_2 # 第一层的第一个的 # dz1_2对da1_1求导 过程是这样的z = wx + b，所以dz1_2对da1_1求导的话结果是w11_2 dz1_2da1_1 = w11_2 # a1_1对dz1_1的求导 da/dz = a(1-a) da1_1dz1_1 = a1_1*(1-a1_1) # dz1_1对dw11_1的求导 dz1_1dw11_1 = x # 这样就求到了第二层第一个神经元对第一层第一个神经元的dw11_1求导 dedw11_1 = deda1_2 * da1_2dz1_2 * dz1_2da1_1 * da1_1dz1_1 * dz1_1dw11_1 # dz/db的求导 z = wx + b，一介函数dz/db的求导为1 dz1_1db1_1 = 1 # 这样就求到了第二层第一个神经元对第一层第一个神经元的db1_1求导 dedb1_1 = deda1_2 * da1_2dz1_2 * dz1_2da1_1 * da1_1dz1_1 * dz1_1db1_1 # 第一层的第二个的 dz1_2da2_1 = w21_2 da2_1dz2_1 = a2_1*(1-a2_1) dz2_1dw12_1 = x dedw12_1 = deda1_2 * da1_2dz1_2 * dz1_2da2_1 * da2_1dz2_1 * dz2_1dw12_1 d2_1db2_1 = 1 dedb2_1 = deda1_2 * da1_2dz1_2 * dz1_2da2_1 * da2_1dz2_1 * d2_1db2_1 # 使用梯度下降进行计算 y = y - alpha * w alpha = 0.03 b1_2 = b1_2 - alpha * dedb1_2 b1_1 = b1_1 - alpha * dedb1_1 b2_1 = b2_1 - alpha * dedb2_1 w11_1 = w11_1 - alpha * dedw11_1 w12_1 = w12_1 - alpha * dedw12_1 w11_2 = w11_2 - alpha * dedw11_2 w21_2 = w21_2 - alpha * dedw21_2 if _ %100 == 0: # 清空窗口 plt.clf() plt.scatter(xs,ys) a1_2,z1_2,a2_1,z2_1,a1_1,z1_1 = forward_propgation(xs) plt.plot(xs,a1_2) # 暂停0.01秒,不暂停看不到绘制图 plt.pause(0.01) ```