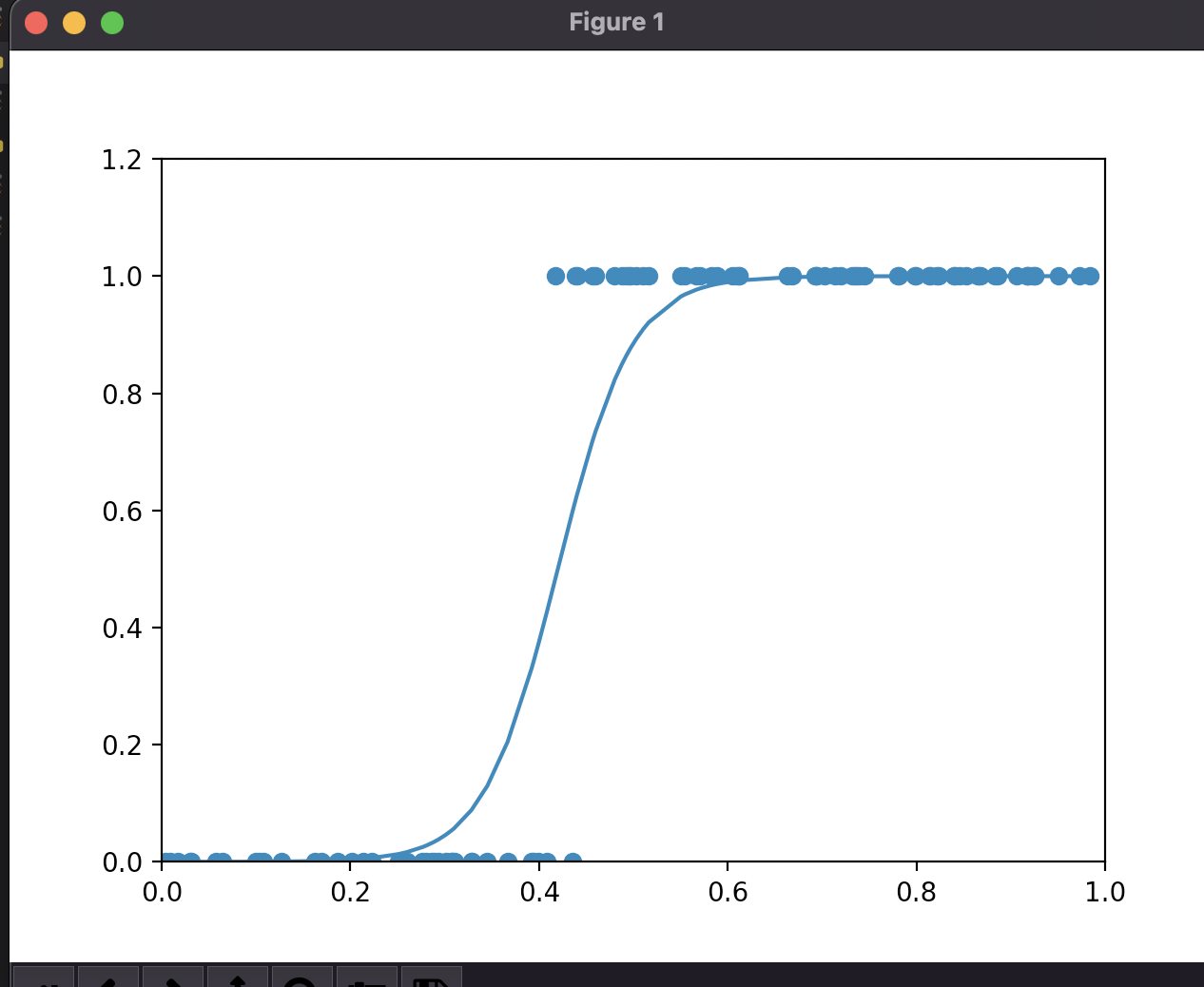
>#python 激活函数分类Logistic函数（学习笔记） [TOC] 前言 ------------ tn2>有时候，我们对某个事物的判断不是1就是0。 举例：我们的吃馒头时一般看馒头多大的就能够判断吃得饱或吃不饱，而不是一个斜线的学习率。 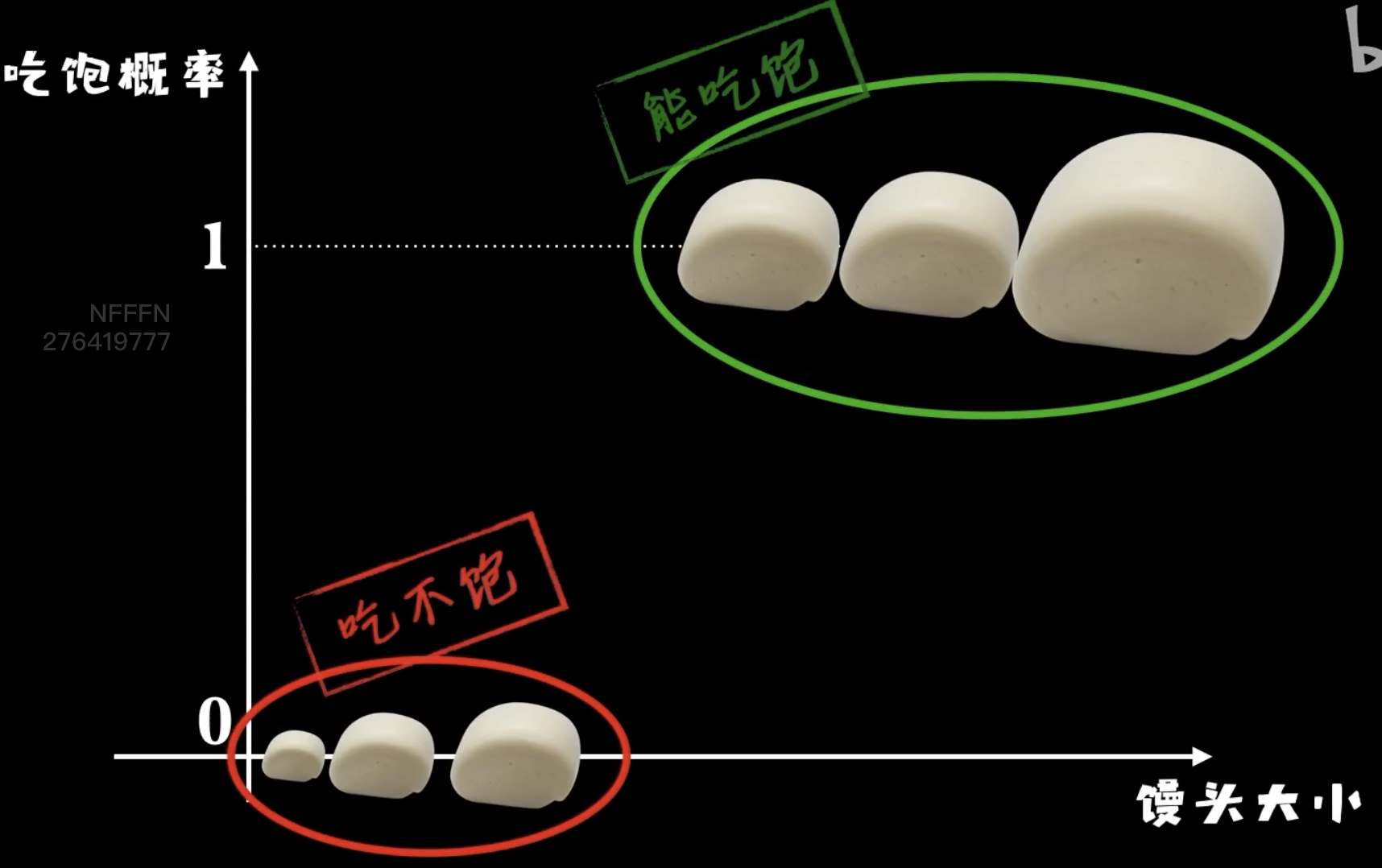 tn>人类思考的方式往往是离散的分类而不是精确的拟合。 tn2>假如小蓝的本身具有一定的抗毒性，比如最多能扛住0.8的毒性，只有超过0.8毒性的才算有毒，其他都算无毒。 如下图所示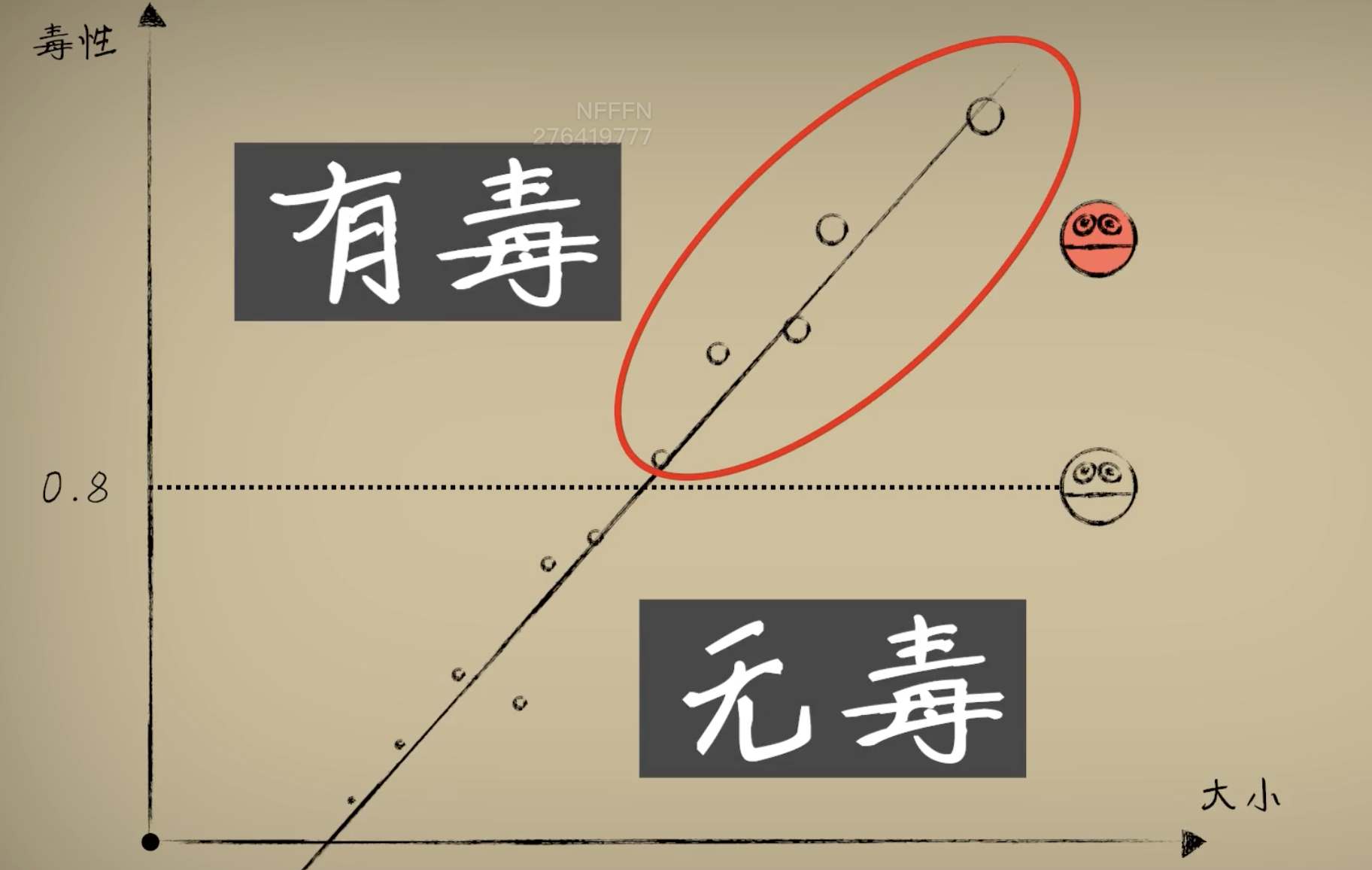：   tn2>那么之前的神经元模型：y=wx + b。 显然不会很有效，我们更希望当有毒性大于某个阈值的时候为1（举例：大于0.8），小于某个阈值的时候为0。 像这样多一个判断的分断函数。  tn2>当然这个函数看着就不是很友好，我们可以的使用s型的Logistic函数来进行处理。 Logistic函数 ------------ tn2>公式如下图所示：  tn2>我们一般取标准的Logistic函数，L为1，k为1，y^0为0。也就是这样。    tn2>它这个函数很适合做判断，并且游很好的韧性。 当a得出z的Logistic函数的结果值时，曲线是不会受到的w值和b值的变化而改变的。  tn2>当a和x形成的曲线伴随着w和b取不同值的时候它们的曲线是会发生变化的。 而调整w和b的方式就是我们之前学的梯度下降算法。  tn2>我们可以通过求导进行梯度下降，然而事实是一个套着一个Sigmoid的函数很复杂，当然我们也可以取两个点来进行求导计算但也比较麻烦。  复合函数求导 ------------ tn2>复合函数求导的过程可以大大的简化我们计算的过程。举例：   tn2>e对w的求导恰好是e对h的求导乘以h对w的求导。 ### 简单解析 tn2>把上面三个de、de、dh看出微分，下面是差值，而到目前为止我们一直在研究一阶导数。 一阶导数具有微分不变性。 所以第一个dh与第二个dh可以看成一样的可以进行约分，就变成了de除以dw，就是e对w的求导。  tn2>e=(y-wx)^2那么h=y-wx ，得出来就是2(y-wx)*(-x)=2x^2w-2xy  tn2>这种求导方式就像拨洋葱，从洋葱的最外层链到最内层，最终得到最外层因变量对最内层的自变量的导数，这就是复合函数的链式法则。  tn2>这里a对sigmoid函数z的求导的过程相当于：1/1+e^-y的求导，求出的导数为`f(y)*(1-f(y))` 代价函数对这种求导的方式就比较轻松了。   tn2>得出e对w和e对b的求导。然后进行梯度下降就很容易了。  tn2>激活函数是非线形的，主要处理越来越复杂的能力。 编程实践 ------------ tn2>修改豆豆的生成。 ```python import numpy as np def get_beans3(counts): xs = np.random.rand(counts) xs = np.sort(xs) ys = np.zeros(counts) for i in range(counts): x = xs[i] yi = 0.7*x+(0.5-np.random.rand())/50+0.5 if yi > 0.8: ys[i] = 1 return xs,ys ``` tn2>进行复合求导训练。 ```python import dataset import matplotlib.pyplot as plt import numpy as np # 获取100个豆豆 xs,ys = dataset.get_beans3(100) # 配置图像 # 设置图像名称 plt.title("Size-Toxicity Function",fontsize=12) # 设置横坐标的名字 plt.xlabel("Bean Size") # 设置纵坐标的名字 plt.ylabel("Toxicity") # 设置散点 plt.scatter(xs,ys) # 设置w为0.1 w = 0.1 # 设置激活函数为0.1 b = 0.1 # 求sigmoid的导数 z = w * xs + b # 求sigmoid的导数 a = 1/(1+np.exp(-z)) plt.plot(xs,a) plt.show() # 5000次学习 for _ in range(5000): for i in range(100): # 获取散点的值 x = xs[i] y = ys[i] # 对w和b求偏导 z = w * x + b # 激活函数 np.exp 表示某数的平方 a = 1/(1+np.exp(-z)) # 方差代价函数 e = (y - a)**2 # 求导 deda = -2*(y - a) dadz = a*(1-a) dzdw = x dzdb = 1 # 再根据复合函数的链式法则得出dedw dedw = deda * dadz * dzdw dedb = deda * dadz * dzdb alpha = 0.05 w = w - alpha * dedw b = b - alpha * dedb # 取余100为0时进行一次绘制这样看着不慢 if _ % 100 == 0: plt.clf() plt.scatter(xs,ys) z = w * xs + b # 求导 a = 1/(1+np.exp(-z)) plt.plot(xs,a) plt.xlim(0,1) plt.ylim(0,1.2) # 暂停0.01秒,不暂停看不到绘制图 plt.pause(0.01) ```