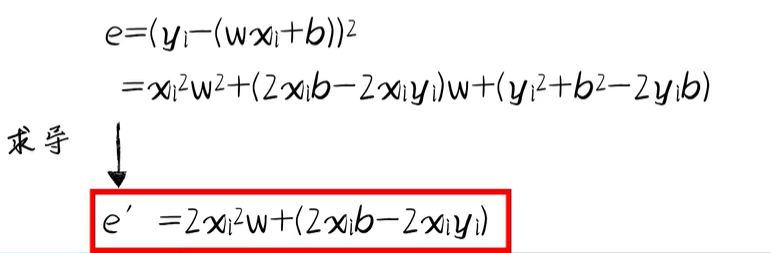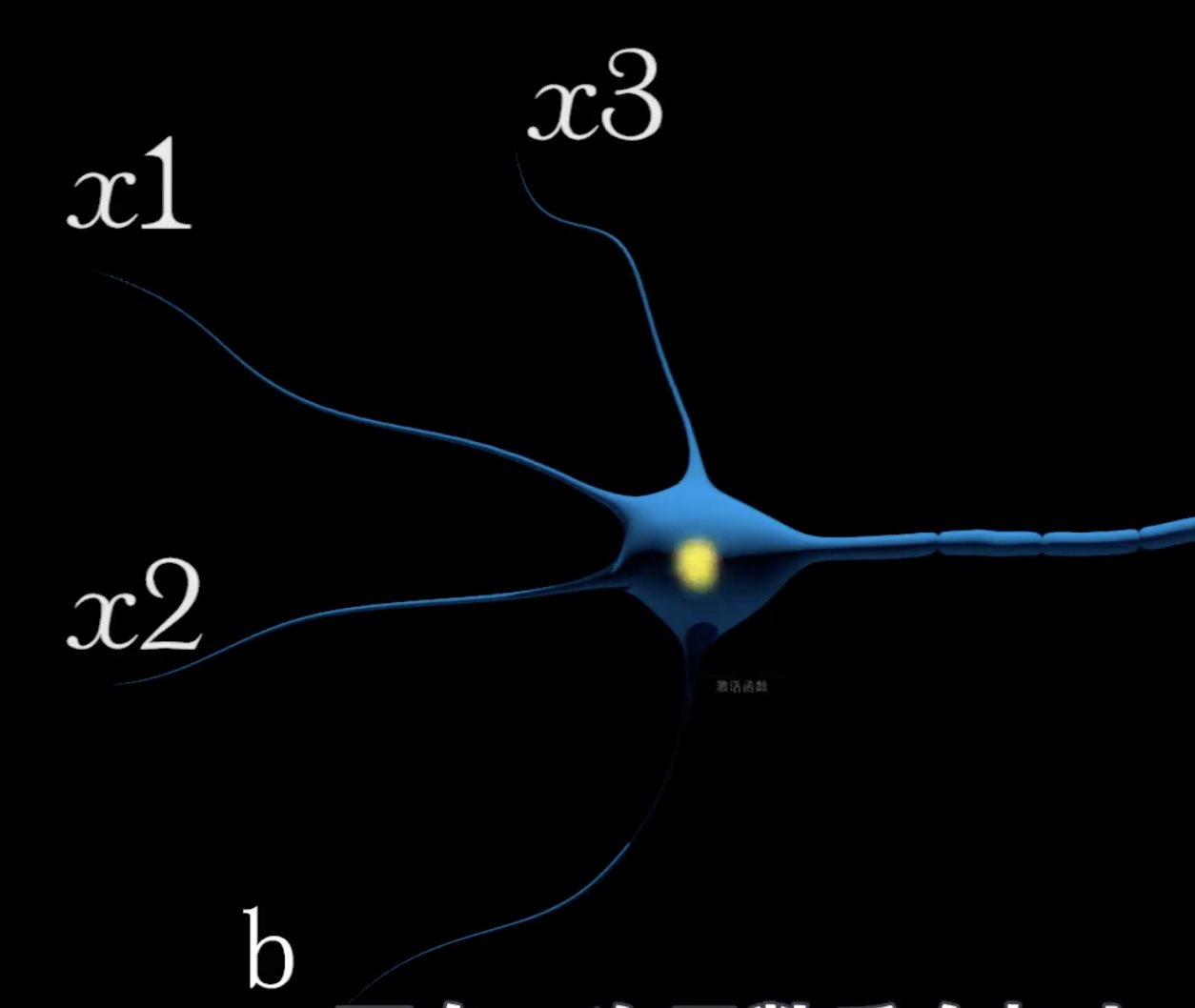>#python 梯度下降和反向传播（下）（学习笔记） [TOC] 前言 ------------  tn2>回到我们以前讲的有一个激活函数b，这是用来干嘛的呢？ 举个例子：有时候豆豆的毒性会随着体积越大而毒性越小，那么此时b所代表的是y毒性自由的移动，w则是毒性。 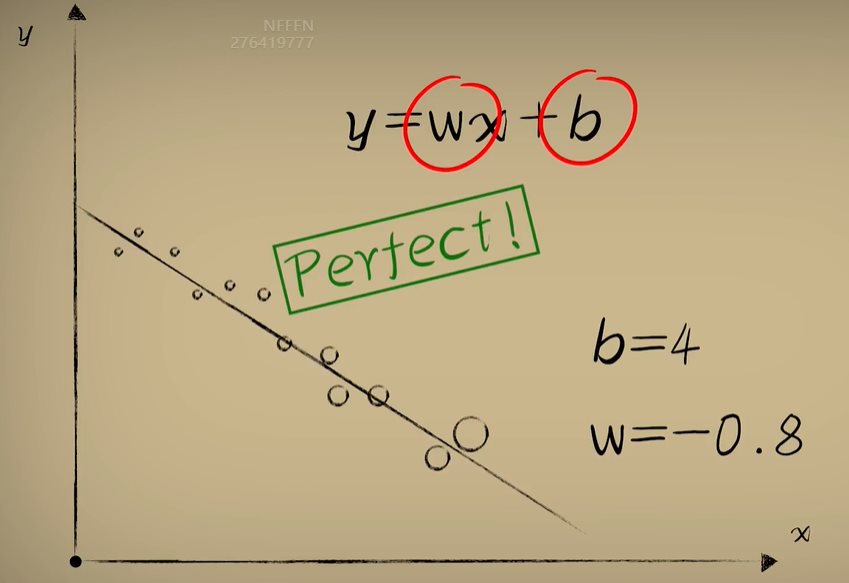 tn2>如果b为0的时候代价函数就是前面几篇中的样子。  tn2>把b当成第三个坐标轴，当我们为b附上值，通过一点点的绘制会形成一个曲线，绘制很多之后就是一个曲面图。   tn2>在这个曲面图的最低点的w和b值放回到预测函数中，会让预测的误差最小。  如何求出最低点？ ------------ tn2>首先我们在e和w的曲面切上一刀，然后通过梯度下降算法调整w，但是你会发现曲线的最低点并不是这个曲面的最低点。   tn2>如果我们在曲面的b和e上也来一刀，我们发现只要将在e和w的曲面上的点，慢慢移动到最b和e上的最低点就比较接近于完美了。  tn2>但事实上这又产生了两次计算，如果把w和b看成一个整体使用空间位移的方式进行一点点的挪动就会慢慢到达底部了。    tn2>由于我们有两个面，所以有两个斜率下降，通过两个面同时下降时的变量称之为偏导数，如果把w和b看作一个向量合起来就是一个新的合向量，沿着这个合向量进行下降的过程称为梯度下降。 所以我们说梯度下降比斜率下降更快。 编程实践 ------------ tn2>首先我们更改一下获取豆豆的变化`dataset.py`。 ```python import numpy as np ... def get_beans2(counts): xs = np.random.rand(counts) xs = np.sort(xs) ys = np.array([(0.7*x+(0.5-np.random.rand())/5+0.5) for x in xs]) return xs,ys ``` ```python # 生成-1到2每次递增加0.1的一组ws ws = np.arange(-1,2,0.1) # 生成-2到2每次递增加0.1的一组bs bs = np.arange(-2,2,0.1) for b in bs: es = [] for w in ws: # 获取预测值 y_pre = w * xs + b # 计算所有样本的均方误差 e = np.sum((ys-y_pre)**2)*(1/m) es.append(e) plt.plot(ws,es) plt.show() # 丝滑 ```  ```python # 获取图形对象 fig = plt.figure() # 创建3D对象 ax = fig.add_subplot(111,projection='3d') # 生成-1到2每次递增加0.1的一组ws ws = np.arange(-1,2,0.1) # 生成-2到2每次递增加0.1的一组bs bs = np.arange(-2,2,0.1) for b in bs: es = [] for w in ws: # 获取预测值 y_pre = w * xs + b # 计算所有样本的均方误差 e = np.sum((ys-y_pre)**2)*(1/m) es.append(e) # 2D # plt.plot(ws,es) # 3D 传入三个坐标轴，zdir表示谁朝上。 ax.plot(ws, es, b, zdir='y') # 散点 # ax.scatter(ws, es, b, zdir='y') plt.show() ``` 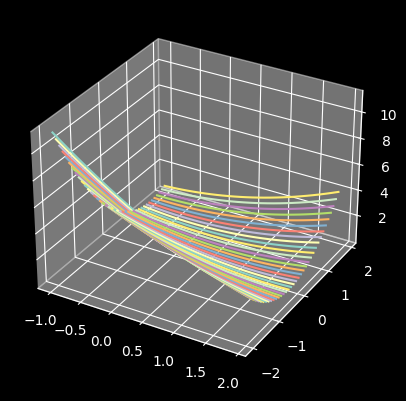 tn2>这里由于z轴的范围太大了，所以我们可以通过`ax.set_zlim(0,2)`设置一下z轴的范围。 ```python fig = plt.figure() # 创建3D对象 ax = fig.add_subplot(111,projection='3d') # 设置垂直范围 ax.set_zlim(0,2) ```  tn2>接下来我们通过代码，进行50000次训练然后同时从b和w进行梯度下降。 ```python # 50000次学习 for _ in range(500): for i in range(100): # 获取散点的值 x = xs[i] y = ys[i] # w曲面进行斜率下降 dw = 2*x**2*w + 2*x*b - 2*x*y # b曲面进行斜率下降 db = 2*b + 2*x*w - 2*y # 设置阿尔法 alpha = 0.01 # 获取新误差值 w = w - alpha * dw # 合梯度下降 b = b - alpha * db # 清除绘图窗口 plt.clf() # 重新绘制 plt.scatter(xs,ys) y_pre = w*xs + b plt.xlim(0,1) plt.ylim(0,1.2) plt.plot(xs,y_pre) # 暂停0.01秒,不暂停看不到绘制图 plt.pause(0.01) ```