>#python 梯度下降和反向传播（上）（学习笔记） [TOC] 基本定义 ------------ tn2>在开始之前我们来学习一些求导（斜率）定义与公式。 ### 求斜率求导（第一种） tn2>当有两个点在一个三角形上，我可以通过如下公式进行求导（斜率）。 简单来讲通过纵坐标的差值除以横坐标的差值就是求导，这种方式也叫定义法。 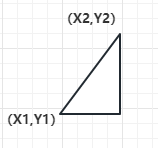 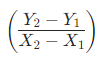 tn2>举例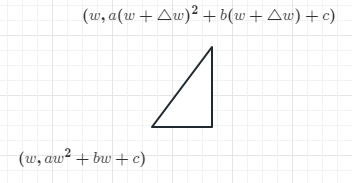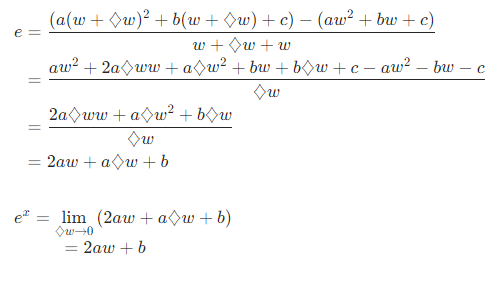：   tn2>这里当取极限为0时，结果为2aw+b ### 求斜率求导（第二种） tn2>求导公式，C表示常函数，X表示冥函数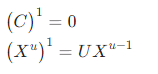：  tn2>求导法则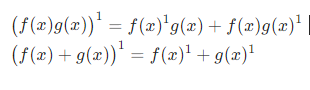：  tn2>计算导数，举例：  tn2>看第一个aw的平方，这里a为常函数导数为0，w的平方为幂函数通过第二个函数得出导数2w。 又根据导数的第一个求导法则得出公式，以及结果为2aw。 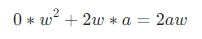  简化计算 ------------ ### 求斜率 tn2>由于我们通过大规模的计算达到一步到位的方式计算量过于复杂，所以我们可以通过挪动的方式来解决这样的问题。 当在中线左边时w不断的增大，当中线在右边时w不断减小。 如下图所示：  tn2>那么通过什么来进行调整呢？ 可以通过斜率来进行调整，当为直线的时候斜率为0，左边的斜率为负数，右边的斜率为正数。 这样我们就可以判断w的值是在最低点的左边还是右边。  tn2>那么我们如果要获得斜率，就需要将一个曲线无限的放大让它趋近于一条直线，那么我们就可以在这上面取两个点并求斜率（也就是求导）。  tn2>需要注意的是，我们在进行直线来求斜率就必须要保证其两条线段的距离足够小？ 足够小是多小啊？他更是数学上讲的极限，当极限值足够小的时候的a^w就为0，得出来的结果`2aw+b`。 这一过程就被称为求导。 简单来讲通过纵坐标的差值除以横坐标的差值就是求导，这种方式也叫定义法。  tn2>还有另一种就是通过求导法则。   ### 每次调整多少合适？ tn2>如果我们每次调整的误差是0.1那么速度上又太慢了。 那么我们可以当w离最低点远时我们可以加快它的调整速度，在快要到达最低点时速度放慢。 如何达到这样的效果呢？当w离开最低点远时，斜率的绝对值就越远，反之w离最低点越近时，斜率的绝对值就越小；为0时就到达了最低点。  tn2>理想很美好，现实很残酷。 当我们通过程序去调整时，w无法调整到最低点，因为调整到幅度太大，所以我们可以通过阿尔法参数来进行误差的调整。  tn2>这种通过曲线不同斜率去调整的方式又被称为梯度下降。 接着我们可以对比一下梯度下降的想法与Roseblat的想法，发现仅仅是多了一步将导数除以了二。 那如何凸显出它的优势呢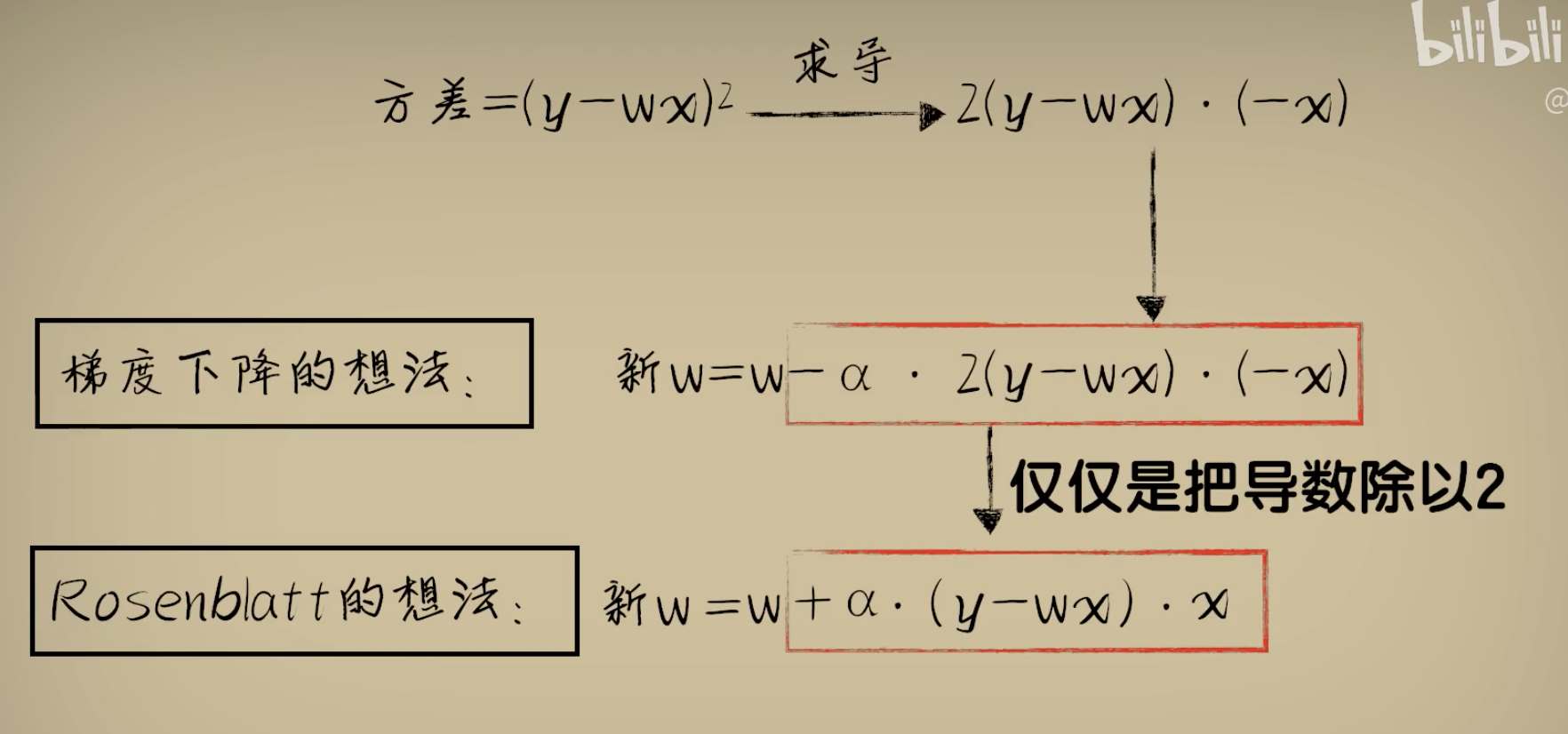？  tn2>正规公式：一次性带入所有的进行计算。 批量梯度下降：使用全部样本进行梯度下降。 随机梯度下降：每次取一个样本进行梯度下降找到最优点。 mini梯度下降：综合上面的优点进行，分批次梯度下降比如一次性100个进行梯度下降。 编程实践 ------------ ### 随机梯度下降算法 ```python import dataset import matplotlib.pyplot as plt import numpy as np # 获取100个豆豆 xs,ys = dataset.get_beans(100) # 配置图像 # 设置图像名称 plt.title("Size-Toxicity Function",fontsize=12) # 设置横坐标的名字 plt.xlabel("Bean Size") # 设置纵坐标的名字 plt.ylabel("Toxicity") # 设置散点 plt.scatter(xs,ys) # 设置权重为0.1 w = 0.1 # 获取预测值 y_pre = w*xs # 按照预测值绘制图案 plt.plot(xs,y_pre) # 显示图案 plt.show() # 10000次学习 for _ in range(100): for i in range(100): # 获取散点的值 x = xs[i] y = ys[i] # 代价函数，e表示平方误差 # e=(y - w * x)^2 = x^2*w^2 + (-2xy)*w + y^2 # a = x^2*w^2 # b = -2xy # c = y^2 # 梯度下降的斜率为k=2aw+b,注意这里w不会算进来因为在刚刚计算时已经省略了 k = 2*(x**2)*w+(-2*x*y) # 设置阿尔法 alpha = 0.1 # 获取新误差值 w = w - alpha * k # 清除绘图窗口 plt.clf() # 重新绘制 plt.scatter(xs,ys) y_pre = w*xs plt.plot(xs,y_pre) # 暂停0.01秒,不暂停看不到绘制图 plt.pause(0.01) ``` 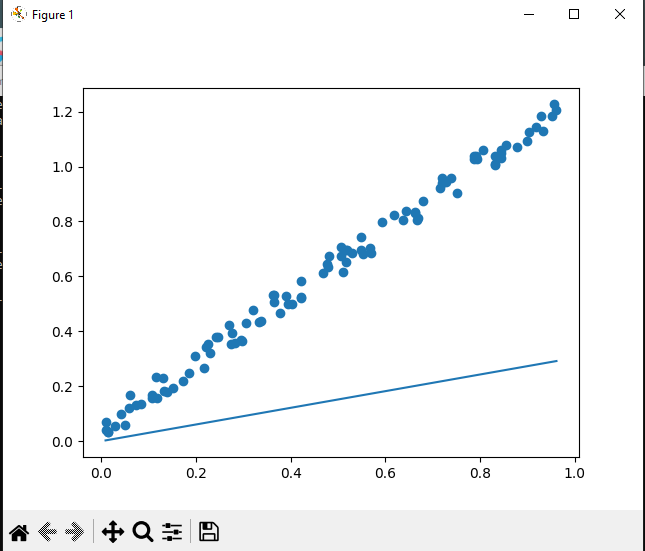 tn2>通过随机梯度下降慢慢的移动到我们想要的位置上，在最后的我们发现它会产生抖动。 其实是由于预测曲线调整的时候触及到比较大的值，就不断的调整坐标的范围。 我们可以通过`xlim`和`ylim`来慢慢调整。 ```python import dataset import matplotlib.pyplot as plt import numpy as np # 获取100个豆豆 xs,ys = dataset.get_beans(100) # 配置图像 # 设置图像名称 plt.title("Size-Toxicity Function",fontsize=12) # 设置横坐标的名字 plt.xlabel("Bean Size") # 设置纵坐标的名字 plt.ylabel("Toxicity") # 设置散点 plt.scatter(xs,ys) # 设置权重为0.1 w = 0.1 # 获取预测值 y_pre = w*xs # 按照预测值绘制图案 plt.plot(xs,y_pre) # 显示图案 plt.show() # 10000次学习 for _ in range(100): for i in range(100): # 获取散点的值 x = xs[i] y = ys[i] # 代价函数，e表示平方误差 # e=(y - w * x)^2 = x^2*w^2 + (-2xy)*w + y^2 # a = x^2*w^2 # b = -2xy # c = y^2 # 梯度下降的斜率为k=2aw+b,注意这里w不会算进来因为在刚刚计算时已经省略了 k = 2*(x**2)*w+(-2*x*y) # 设置阿尔法 alpha = 0.1 # 获取新误差值 w = w - alpha * k # 清除绘图窗口 plt.clf() # 重新绘制 plt.scatter(xs,ys) y_pre = w*xs plt.xlim(0,1) plt.ylim(0,1.2) plt.plot(xs,y_pre) # 暂停0.01秒,不暂停看不到绘制图 plt.pause(0.01) ``` ### 批量梯度下降 tn2>直接通过sum计算出所有的梯度下降。 ```python # 10000次学习 for i in range(100): # 获取散点的值 x = xs[i] y = ys[i] # 代价函数，e表示平方误差 # e=(y - w * x)^2 = x^2*w^2 + (-2xy)*w + y^2 # a = x^2*w^2 # b = -2xy # c = y^2 # sum 总计算一百次 k = 2*np.sum(x**2)*w+(-2*x*y) w = w - alpha * k plt.clf() plt.scatter(xs,ys) y_pre = w*xs plt.plot(xs,y_pre) plt.pause(0.01) ``` ### 固定步长下降 tn2>就是0.1，0.1的靠近。 ```python # 设置阿尔法 alpha = 0.1 step = 0.01 # 10000次学习 for i in range(100): # 获取散点的值 x = xs[i] y = ys[i] # sum 总计算一百次 k = 2*np.sum(x**2)*w+(-2*x*y) k = k/100 if k > 0: w = w - step else: w = w + step y_pre = w*xs # 预测 plt.clf() plt.xlim(0,1) plt.ylim(0,1.2) plt.scatter(xs,ys) plt.plot(xs,y_pre) plt.pause(0.01) ``` 小结 ------------ tn2>通过这三次的观察，发现随机梯度下降算法比较可观。