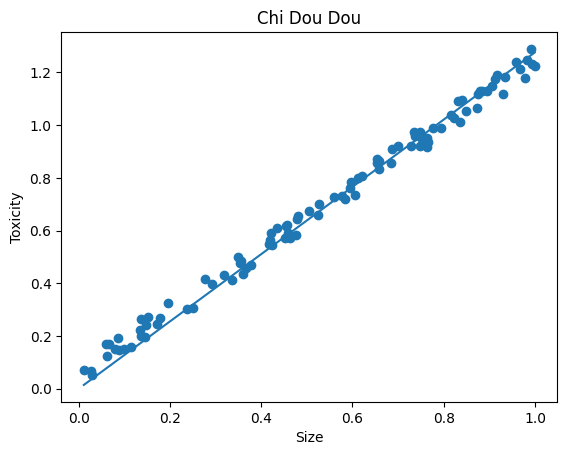
>#python 方差代价函数（学习笔记） [TOC] tn2>在Rosenblatt感知器中计算有个问题？ 如果只有两个豆豆的情况下，且二者都相差`0.15`一个是正数一个是负数，所以体现的误差值为0。 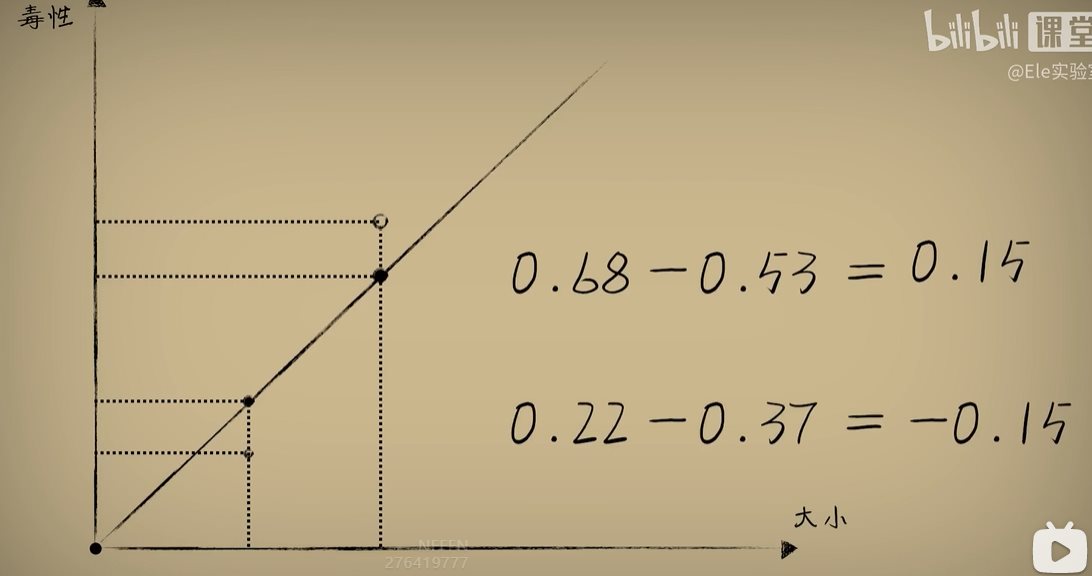 绝对差 ------------ tn2>通过把值进行绝对值的处理产生绝对差，使他们都相差`0.15`. 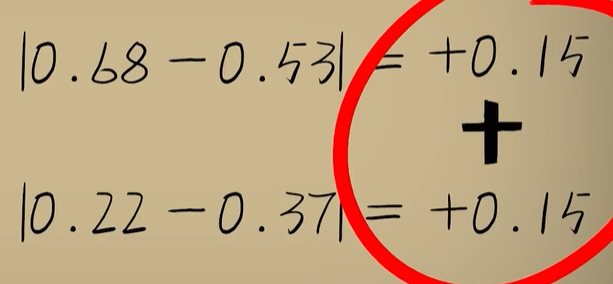 tn2>但是绝对值在绝对差处理上都不是很方便。所以人们提出了平方误差。 平方误差 ------------ tn2>通过将误差的值进行平方处理，就是平方误差。 平方误差越小说明，得出的结果就越接近真相。 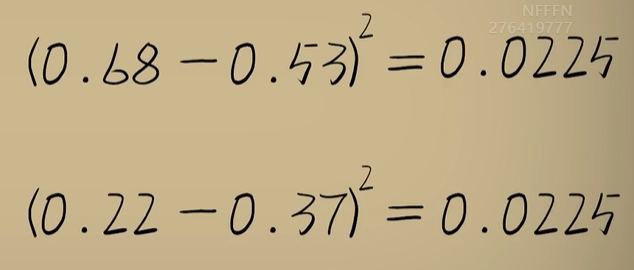 tn2>而我们知道是参数w决定了预测函数的样子，如果把误差与w之间的关系画出来就是一个一元二次函数。  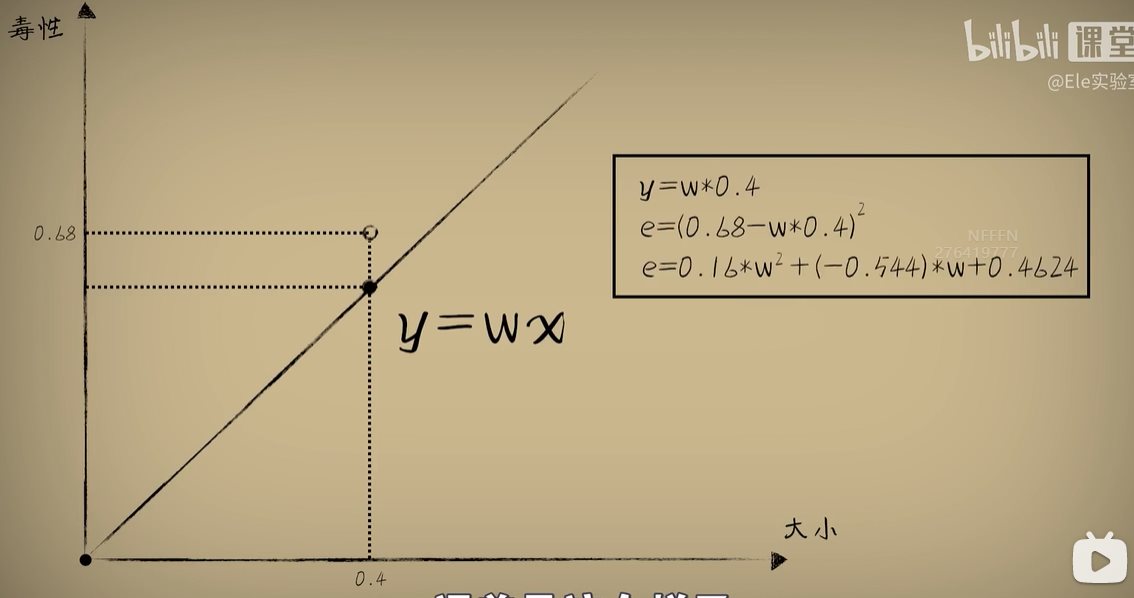 tn2>这里通过单个豆豆来举例，公式就是`e=a*w2+b*w +c`（a是0.16、b是-0.544、c是0.4624）。 如果是一组豆豆也是一样的，可以通过把所有的豆豆的平方误差相加然后取平均数，这一过程也叫均方误差。 简化后如下图所示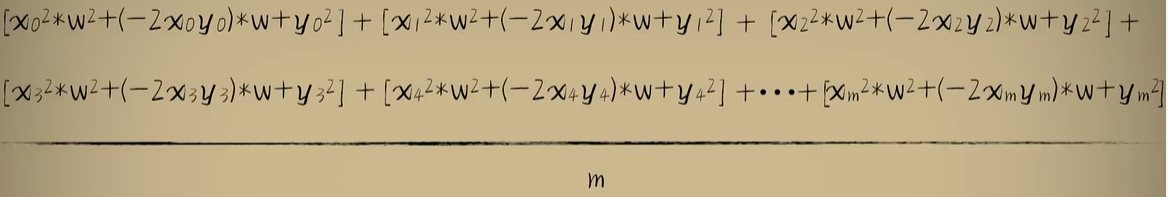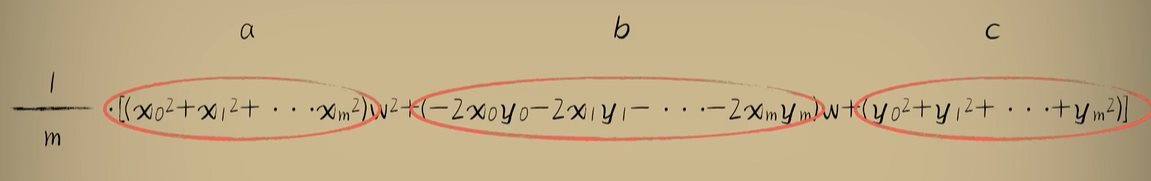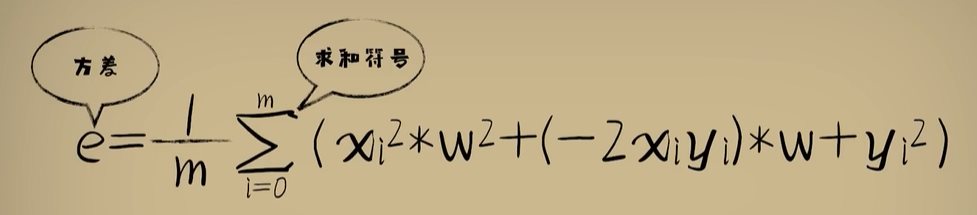：    tn2>得到公式后，我们只需要让机器计算得到一元二次方程的顶点，就是最好的误差。 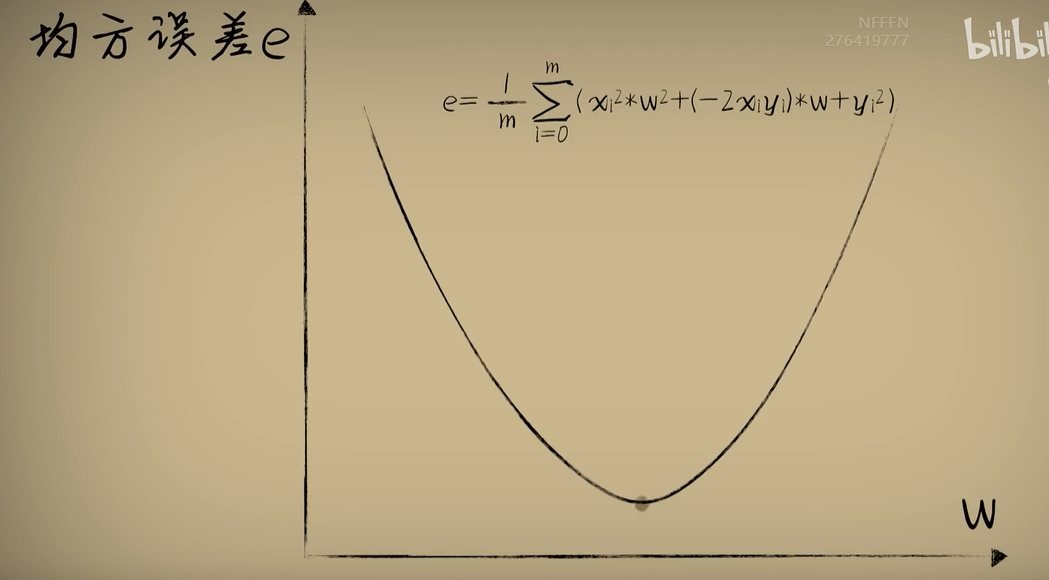 tn2>所以我们可以通过顶点坐标公式来求，最后简化出来如下图所示。 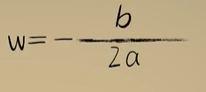 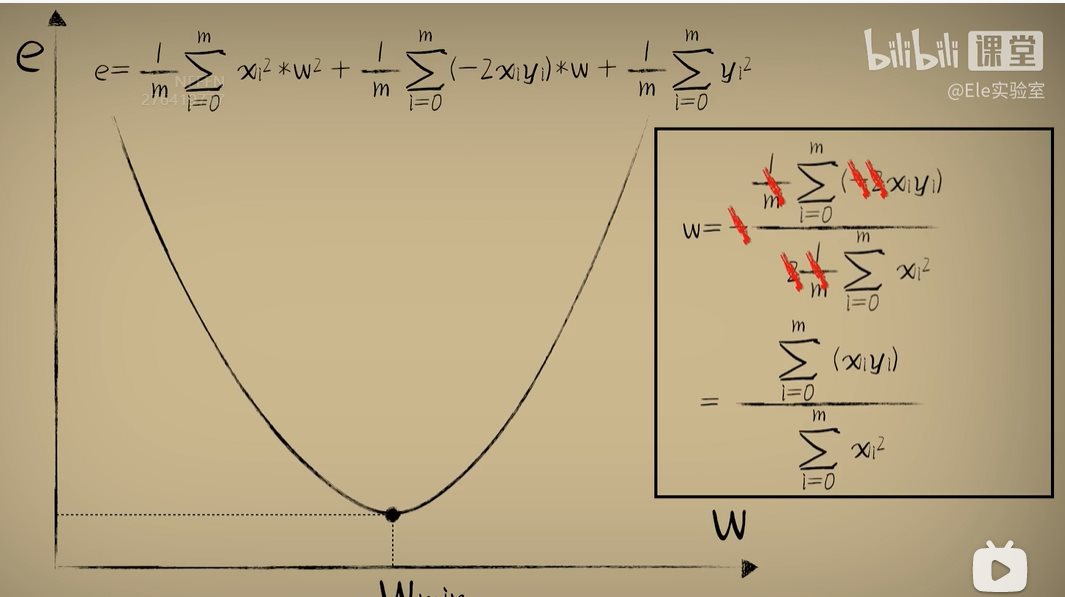 正规方程 ------------ tn2>一次性求出误差最小处的w取值。 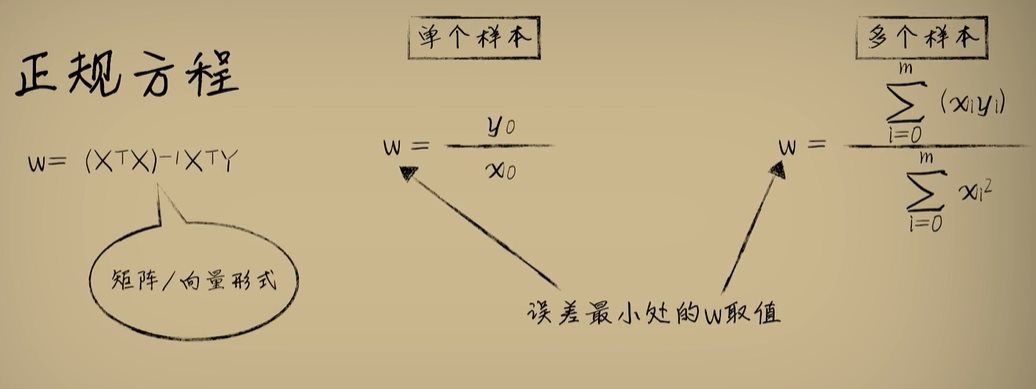 tn2>那么直接这样计算就万事大吉了吗？在少量数据的时候确实是这样，但数据量大举例1000个维度就要10亿次。 如何解决呢？可以查看下一篇的梯度下降。 编程实践 ------------ tn2>首先我们初始化豆豆的思考。 ```python # 导入散点数据库 import dataset # matplotlib库 import matplotlib.pyplot as plt # 导入numpy库 import numpy as np # 创建一些散点数据 xs,ys = dataset.get_beans(100) # 配置图像 plt.title("Chi Dou Dou",fontsize=12)# 设置图像名称 plt.xlabel("Size")# 设置横坐标名称 plt.ylabel("Toxicity")# 设置纵坐标名称 # 把值负到图上 plt.scatter(xs,ys) # 初始化设置w为0.1权重 w = 0.1 # 得到预测值 y_pre = w*xs # 画图并展示 plt.plot(xs,y_pre) plt.show() ``` 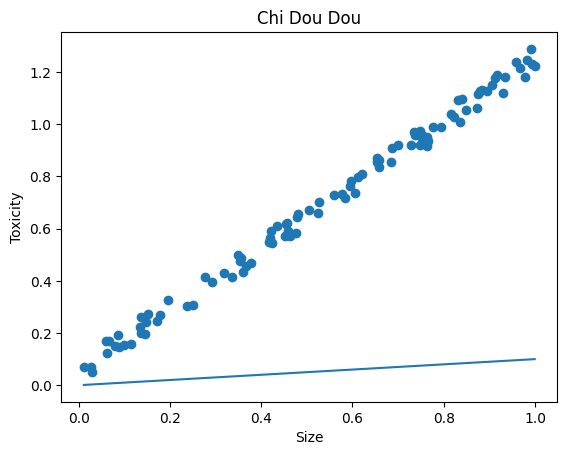 tn2>然后我们更具均方差求出一元二次方程的均方差与权重的图。 ```python # 获取均方差 es = (ys-y_pre)**2 # 算出最优误差顶点，总数和除以总数量 es_sum = np.sum(es) es_len = len(es) es_sum = es_sum / es_len # 显示误差值与权重的二元一次方程 # 配置图像 plt.title("Cost Function",fontsize=12)# 设置图像名称 plt.xlabel("w")# 设置横坐标名称 plt.ylabel("e")# 设置纵坐标名称 # 设置不同的权重带入预测函数的运算 # 起始值，结束值，递进大小 ws = np.arange(0,3,0.1) # 均方误差集合 es = [] for w in ws: # 获取预测值 y_pre = w * xs # 获取误差 e = np.sum((ys-y_pre)**2) / es_len # 输出 es.append(e) plt.plot(ws,es) plt.show() ``` 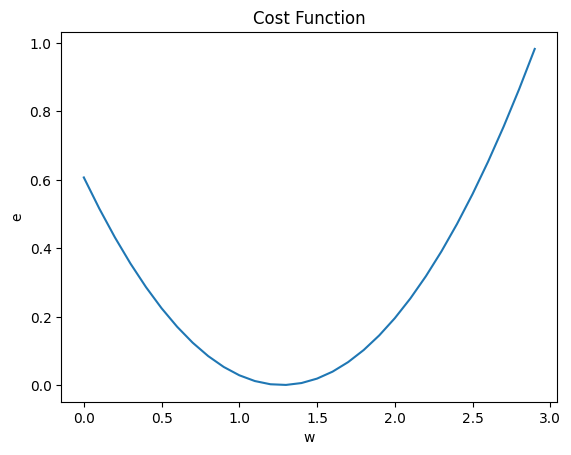 tn2>接下来通过所有的最小点来设置权重值。 求一元二次方程的最低点，也就是我们刚刚讲的顶点坐标公式。 ```python w_min = np.sum(xs*ys)/np.sum(xs*xs) # e的最小点w，str表示格式化成字符串 print("e的最小点w："+str(w_min)) # 计算所有豆豆的最佳值 y_pre = w_min * xs # 打印图形 # 配置图像 plt.title("Chi Dou Dou",fontsize=12)# 设置图像名称 plt.xlabel("Size")# 设置横坐标名称 plt.ylabel("Toxicity")# 设置纵坐标名称 # 把值负到图上 plt.scatter(xs,ys) plt.plot(xs,y_pre) plt.show() ```