>#python 选择和训练模型（三） [TOC] tn2>请根据上一篇结合。 训练和评估训练集 ------------ tn2>使用sklearn的LinearRegression（线性回归）、DecisionTreeRegressor（决策数）、 ### 线性回归  tn2>首先添加两句话，在预测房价之前 ```python housing = strat_train_set.drop("median_house_value", axis=1) housing_labels = strat_train_set["median_house_value"].copy() ``` tn2>然后在末尾添加如下代码进行RMSE的计算。 ```python from sklearn.linear_model import LinearRegression # 创建实例 lin_reg = LinearRegression() # 训练 lin_reg.fit(housing_prepared, housing_labels) # 找训练集里面后5条数据 some_data = housing.iloc[:5] some_labels = housing_labels.iloc[:5] # 用模型转换一下 some_data_prepared = full_pipeline.transform(some_data) print("Predictions:",lin_reg.predict(some_data_prepared)) print("Labels:",list(some_labels)) ```  tn2>我们可以看到预测值与实际值还是有一定的差距，RMSE还需要取平方根。 ```python from sklearn.metrics import mean_squared_error # 接收一个numpy数组 housing_predictions = lin_reg.predict(housing_prepared) # 计算均方误差 lin_mse = mean_squared_error(housing_labels,housing_predictions) # 计算均方根误差 lin_rmse = np.sqrt(lin_mse) lin_rmse ```  tn2>误差6.8w。 ### 决策数 ```python from sklearn.tree import DecisionTreeRegressor tree_reg = DecisionTreeRegressor() tree_reg.fit(housing_prepared, housing_labels) housing_predictions = tree_reg.predict(housing_prepared) tree_mse = mean_squared_error(housing_labels,housing_predictions) tree_rmse = np.sqrt(tree_mse) tree_rmse ``` tn2>误差得出来是0  ### 使用交叉验证来更好的评估 tn2>一个选择是sklearn的K-fold交叉验证功能。 原理：先将训练集分割成十个不同的子集，每一个子集分割成一个fold。然后通过决策树模型进行十次训练与评估，每次挑选一个进行评估，九个进行训练，产生的结果就是一个包含十次结果的数组。 ```python from sklearn.model_selection import cross_val_score scores = cross_val_score(tree_reg, housing_prepared, housing_labels,scoring="neg_mean_squared_error", cv=10) tree_rmse_scores = np.sqrt(-scores) # 帮助函数 def display_scores(scores): # 源数据 print("Scores:", scores) # 平均数 print("Mean:", scores.mean()) # 标准差 print("Standard deviation:", scores.std()) display_scores(tree_rmse_scores) ```  tn2>通过它我们看到它比线性回归模型还要糟糕。 ### 随机森林回归 ```python from sklearn.ensemble import RandomForestRegressor forest_reg = RandomForestRegressor() forest_reg.fit(housing_prepared, housing_labels) housing_predictions = forest_reg.predict(housing_prepared) forest_mse = mean_squared_error(housing_labels, housing_predictions) forest_rmse = np.sqrt(forest_mse) forest_rmse ```  ### 交叉验证 ```python scores = cross_val_score(forest_reg, housing_prepared, housing_labels,scoring="neg_mean_squared_error", cv=10) forest_rmse_scores = np.sqrt(-scores) display_scores(forest_rmse_scores) ``` 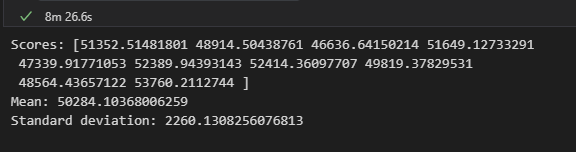 调优模型 ------------ tn2>GirdSearchCV、随机搜索、集成方法、分析最佳模型和误差、使用测试集来评估系统。 ### 超参数Hyperparameter tn2>模型参数。例如 y = ax + b,通过训练得到的参数 超参数：需要人为设定。是开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。 ### GridSearchCV tn2>可使用GridSearchCV来搜索超参数 你只需要告诉它你要进行实验的超参数是什么，以及需要尝试的值，它会使用交叉验证来评估超参数值的所有可能组合。 ### 随机搜索 tn2>如果超参数的搜索范围较大，可选择RandomizedSearchCV ### 集成方法 tn2>还有一种调优方法是将表现最优的模型组合起来，通常比单一模型好。 ### 使用测试集来评估系统 ```python X_test = strat_test_set.drop("median_house_value",axis=1) y_test = strat_test_set["median_house_value"].copy() X_test_prepared = full_pipeline.transform(X_test) # 随机森林 final_predictions = forest_reg.predict(X_test_prepared) final_mse = mean_squared_error(y_test, final_predictions) final_rmse = np.sqrt(final_mse) final_rmse ``` 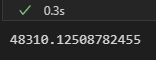 启动、监控、维护你的系统 ------------ tn2>将模型部署到生产环境：一种方法是保存训练好的模型（使用joblib），包括预处理和流水线，然后在生产环境中加载该模型，并调用prepare()方法来预测。